导语

2024年诺贝尔物理学奖授予“通过人工神经网络实现机器学习的基础性发现和发明”，引发人们对统计物理与机器学习之间深刻联系的关注和广泛讨论。机器学习能为物理学做些什么？物理学又能为机器学习做些什么？近期 PNAS 杂志发表「物理学遇见机器学习」（Physics Meets Machine Learning）主题特刊，展现了物理学与机器学习两个领域之间的活跃对话，论文主题涵盖生物物理与机器学习、动态学习系统、生成模型、表征与泛化、神经标度律等各个方向。本文翻译自美国东北大学物理系与生物工程系杰出教授 Herbert Levine 与IBM 沃森研究中心研究员涂豫海撰写的特刊引言，文章认为，人工神经网络受益于统计物理学和神经科学这两个自然科学学科，深度学习的下一个突破可能来自基于统计物理学概念和方法建立的坚实理论基础，而探索真实大脑计算与深度学习神经网络之间的差异，可能会产生新的脑启发算法。

为了深入探索统计物理前沿进展，集智俱乐部联合西湖大学理学院及交叉科学中心讲席教授汤雷翰、纽约州立大学石溪分校化学和物理学系教授汪劲、德累斯顿系统生物学中心博士后研究员梁师翎、香港浸会大学物理系助理教授唐乾元，以及多位国内外知名学者共同发起。读书会旨在探讨统计物理学的最新理论突破，统计物理在复杂系统和生命科学中的应用，以及与机器学习等前沿领域的交叉研究。读书会从12月12日开始，每周四晚20:00-22:00进行，持续时间预计12周。我们诚挚邀请各位朋友参与讨论交流，一起探索爱因斯坦眼中的普适理论！

关键词：统计物理，机器学习，深度学习神经网络，随机学习动力学，损失景观，泛化，神经科学

Herbert Levine，Yuhai Tu（涂豫海）| 作者

吴晨阳| 译者

梁金 | 审校

论文题目： Machine learning meets physics: A two-way street 论文地址： https://www.pnas.org/doi/10.1073/pnas.2403580121

目录

1. 机器学习与蛋白质折叠问题

2. 机器学习的拓展

3. 物理能为机器学习做什么？

3.1 机器学习的中心法则

3.2 随机学习动力学：从涨落的损失景观上滚落

3.3 泛化：高维的祝福与诅咒

本文介绍了一期特刊，这期特刊关注迅速发展的机器学习 （machine learning， ML） 领域与物理学研究之间的互动。特刊上半部分论文讨论了机器学习能为物理学做些什么，下半部分论文则探讨了物理学能为机器学习做些什么。正如我们将看到的，这两个方向都在活跃地发展。

物理学是一个非常广阔的学科，几乎每个分支都在探索机器学习的潜在应用。我们显然无法系统地涵盖所有这些发展。相反，我们将呈现各种示例，并尝试提出一些初步的总体见解。鉴于研究活动的巨大热潮，我们确信这些观点需要随着经验的积累不断修正。尽管如此，我们仍将继续。

1. 机器学习与蛋白质折叠问题

在根据序列确定蛋白质结构方面，AlphaFold [1]及其后续版本的表现堪称机器学习解决重要物理问题的典范。这是一个在生物物理学领域研究了多年的问题 [2-4]，该领域的研究者积极参与了一个被称为结构预测关键评估 （the Critical Assessment of Structural Prediction， CASP） 的两年一度的竞赛，其中各种方法都会与已知但尚未公布的数据进行对比评估。一个重要的里程碑是 AlphaFold 在2018年竞赛的总排名中位列第一，并在2020年再次重复了这一成就。到2022年第十五届 CASP 竞赛时，大多数参赛者都在其方法中采用了某种基于 AlphaFold 的理念。该方法已经变得如此普遍，以至于这个词已经开始被用作动词，例如“Can we AlphaFold our way out of the next pandemic?” （我们能否用 AlphaFold 摆脱下一次大流行？） [5]。本期特刊中 Park 等人[6]的论文为如何在现代计算系统上有效地使用 AlphaFold2 提供了一个实用指南。

从蛋白质折叠应用的历史中可以获得一些有趣的启示。我和 Terry Sejnowski 两人在20世纪80年代末都在加州大学圣地亚哥分校 （UCSD） ，当时他做了一个论文报告，是关于使用神经网络研究球状蛋白的二级结构[7]。他的算法性能相当平庸，我们中的许多人在离开那次讲座时都在想，为什么有人会放弃传统的生物化学方法，而青睐我们现在称之为机器学习的方法。那么，从那时到2018年这30年间发生了什么？似乎有四个因素在起作用。

首先，用于解决这个问题的计算能力以几乎难以想象的速度增长。例如，1985年左右的 Cray 2 超级计算机作为那个时代最快的计算机，运算速度达到1.9千兆浮点运算每秒 （gigaflops） ；而现在这大约相当于 iPhone 4 的计算能力。当下最先进的超级计算机运算能力已达到109千兆浮点运算每秒。在当时完全无法实现的计算，现在已变得轻而易举。关于内存容量也可以举出类似的数据。可以说，如果相关研究人员未能获得这些计算能力，那么研究进展将会受到极大阻碍。

硬件改进是必要的，但还不够。第二个因素是各种机器学习技术的发明，从而能够从现有数据中学习预测模型。由于未能认识到 Minsky 和 Papert 在感知机研究中提出的著名的“否定性” （no-go） 结论[8]的严重局限性，神经网络领域在20世纪80年代仍处于低迷期。那时，人们才刚刚意识到带有隐藏层的“深度网络”可能开创新局面，这一进展始于玻尔兹曼机 （Boltzmann machine） [9]等结构的出现，并在随后发展出了反向传播训练算法[10]。如今，transformer 架构[11]、自编码器[12]和对抗网络[13]等理念已经彻底改变了人们对机器学习过程的理解。就 AlphaFold 的例子而言，transformer 理念似乎是绝对必要的。Martin 等人[15]的论文讨论了 transformer 如何与更一般的机器学习概念相结合，这些概念可以追溯到 Hopfield 联想记忆模型[14]。

下一个因素是训练所需的数据可用性。蛋白质数据库 （PDB） 成立于1971年，用于存储蛋白质结构信息 [16]。同样，可供所有研究人员使用的结构数据量出现了爆炸性增长。结构数量大约每6到8年翻一番；到2024年初，PDB 数据库已超过20万个结构，相比之下1990年仅有约1000个结构；参见图1。但这并不是唯一重要的数据来源。正如 Martin 等人 [15] 的文章所述，蛋白质折叠领域的许多进展源于这样一个认识：通过比较不同生物体中同一蛋白质的序列，可以获得有关接触图谱 （contact map） 的重要信息。接触图谱是一种矩阵表示，显示了沿主链相距较远的残基在折叠结构中可能在三维空间中靠近的概率。这里的核心思想源于直接耦合分析 （direct coupling analysis，DCA） [17, 18] 等算法的研究，即，从一个物种到另一个物种的演化过程中，一对接触的残基必须共同进化以维持这种接触。因此，对相关进化的观察可以帮助识别这些接触。得益于测序领域令人惊叹的技术进步，过去十年中比较基因组学数据呈现出海啸般的增长。

图1. 2019年蛋白质数据库（PDB）核心档案库增长报告。每个柱状图的总高度表示累计发布的结构总数，柱状图中不同颜色代表不同的实验技术（MX（大分子晶体学）-绿色、3DEM（三维电子显微镜）-黄色、NMR（核磁共振）-蓝色）。引自参考文献[16]。

最后一个，可能也是最有趣的因素，这个问题对机器学习研究的未来发展有着重要影响。问题是：过去三十年使用传统技术对蛋白质折叠进行的大量理论研究，到底有多重要？更简单地说，如果在一个平行宇宙中，在 AlphaFold 时代之前没有人关注蛋白质折叠计算，我们现在的研究进展会落后多少？当然，这个问题不可能有确切答案，但我们认为理论研究确实是当前进展得以实现的重要推手。我们已经提到，使用比较基因组学数据的想法就源于理论研究群体。一个同样重要的想法是将结构数据编码到标准生物物理模型中[19]，这种方法既利用了物理洞见又运用了测量信息。此外，由氨基酸序列预测蛋白质结构作为蛋白质折叠在工程应用方面的进步，不应与最小阻挫 （minimal frustration） [20]、折叠漏斗 （folding funnel） [21] 等概念所带来的蛋白质折叠理论进步混为一谈。这些概念的重要性是全局的，在其他的背景下也有应用，包括分子水平 [22, 23] 和细胞水平 [24]。而且，即使从纯实用的角度来看并非必需，拥有“人类可理解的”方法有时也是很好的。

这一研究方向当前面临哪些挑战？首先是那些不存在唯一结构的系统，在这些系统中，折叠问题转化为寻找一个结构集合以及与之相伴随的结构之间转换的动力学。这类系统包括内在无序蛋白质 （intrinsically disordered proteins） [25] 以及基因组折叠 [26, 27]。另一个方向涉及生物分子相互作用的研究，其中 Alpha-Multimer 的纯机器学习方法在许多应用中尚未被证明足够可靠。Lupo 等人的论文 [28] 试图通过应用语言模型来更好地对齐蛋白质-蛋白质界面处相关的相互作用序列，以解决这个问题。此外还应当注意到T细胞受体对抗原的识别问题，这种抗原识别是适应性免疫系统的关键组成部分。在这方面，最近的研究[29, 30]则通过使用语言模型来解决这个问题，与之竞争的还有混合方法[31]，这类方法整合了结构数据但也因此会受到结构数据缺乏的限制。

2. 机器学习的扩展

生物物理学是探索机器学习应用的一个自然途径。与物理学的其他许多领域不同，大多数与生命世界相关的实验系统都极其复杂，因此从第一性原理建立模型的能力相当有限。以分子尺度之上的一个例子来说，不可能有任何第一性原理模型能够恰如其分地处理细胞集体运动 [32] 所涉细胞机制的全部复杂性。这里没有纳维-斯托克斯 （Navier–Stokes） 方程可以来救场，因此人们自然会思考，是否可以用纯数据驱动的模型来有效替代手工构建的模型[33, 34]。研究者们正在多个细胞运动实验系统 [35, 36] 中积极研究该问题，当然，许多生物医药领域的工作也在深入研究该问题，例如数字病理学方面的工作 [37]。值得注意的是，我们可以尝试通过机器学习来推导出更好的手工模型 （参见文献38） ；但目前尚不清楚为什么这样做会比直接使用学习到的神经网络预测结果更好。

比起上述情况，或许更令人惊讶的是，机器学习方法正在渗透到那些名义上具有可靠计算框架的物理系统研究中。Yu 和 Wang 的论文 [39] 很好地总结了这些系统。一种观点认为，即使在有第一性原理模型可用的情况下，机器学习也可以加速计算。Kochkov 等人 [40] 就持有这种观点，他们明确关注前面提到的用于流体动力学的纳维-斯托克斯方程。也许在那些原则上可知但可能过于复杂而难以实现的物理问题中，这种方法会更有说服力；气候模拟器中的云模型可能就是这样一个例子。总体上看，在结合传统建模的可解释性与机器学习的泛化能力方面，似乎还有很大的进步空间。

如果我们关注于某个非常具体的物理系统的模型，为获得有意义的结果，通常必要的大规模计算是可以承受的；并且，随着计算能力持续指数增长，这变得越来越容易。然而，正如 King 等人 [41] 在本期关于材料组装的论文中所强调的那样，当任务是设计新事物时，这会变得困难得多。这个挑战需要一个迭代过程，即在微观尺度上选择相互作用，并最终在更大尺度上产生某种功能性行为。这个迭代过程通常涉及某种功能性度量 （measure） 的梯度下降，但作为收敛过程的一部分，“正向”问题必须被计算多次。正如该论文所讨论的，这个问题可以通过机器学习的思想得到极大改善，包括自动微分[42]的概念，它能够将大尺度误差“反向传播”到微观自由度的必要改变中。当然，这个思想原本是神经网络模型中训练隐藏层的算法核心，但现在，这个理念可以自动应用于任何大规模计算。

当人们思考机器学习及其在物理学中的应用时，弦论可能不会立即浮现在脑海中。然而，弦论研究者们正在积极探索机器学习方法是否有用[43]。当然，弦论试图构建一个“万物理论”，通过存在于11维空间中的“弦” （一维延展的量子对象） 来解释所有基本粒子及其相互作用。机器学习被用来寻找方法将这个11维空间压缩到我们体验的4维世界。寻找合理的紧致化是一个非常困难的计算问题，而这可以通过机器学习的理念得到改善。谁知道呢？

在机器学习与物理学 （ML-Physics） 交叉领域，还有最后一个正在研究的方向。一些研究组正在尝试使用机器学习方法从数据中自动发现新方程；想象一下，利用行星数据来尝试同时学习牛顿运动定律和引力的平方反比定律。这个想法在Yu[39]的论文中有简要概述，并提供了相关参考文献。我们可以将这项努力视为试图最终将理论物理学家用其人工智能版本取代。不过在机器能够观察天体物理数据并发现正确的理解框架是四维时空中的黎曼几何之前，我们对自己的工作还不用担心。

3. 物理能为机器学习做什么？

当然，机器学习的影响远不止于推进物理科学。深度学习神经网络 （Deep learning neural network， DLNN） 模型 [44, 45] 在图像识别[46]、机器翻译[47]、游戏[48]等领域取得了一连串快速而巨大的成功，而且正如我们已经讨论过的，甚至解决了蛋白质折叠[1]这样长期存在的重大科学挑战。无论好坏，像ChatGPT这样的最新生成模型正从根本上改变着我们这个时代的社会、经济和政治格局。

然而，最近深度学习神经网络令人难以置信的成功产生了一个副作用，即人们为了追求快速、狭隘的应用驱动型发展，而忽视了其理论动机和基础。这正在逐渐导致越来越多的次优实践，包括在缺乏理论指导的优化和正则化步骤 （optimization and regularization procedure） 所涉及的大量超参数上耗费大量计算和时间进行调优，对高精度编码参数的低效利用，对昂贵标记数据的低效利用，最终结果缺乏可重复性，以及滥用这项强大技术的可能性。发展过参数化连接主义机器学习模型 （如深度学习神经网络） 的理论基础，将有助于避免此类问题，从而简化其优化过程，并实现用更少数据训练出稳健模型。同时，规范性理论提供的预测可以指导改进未来的架构和训练范式。

人工神经网络 （Artificial neural network，ANN） 模型源于统计物理学和神经科学这两个自然科学学科的结合。从本质上讲，人工神经网络描述了一组高度抽象的“神经元”在网络中通过自适应方式相互作用而产生的涌现 （集体） 行为，这种网络与大脑中的真实神经网络有某些相似之处。模型动力学使人工神经网络能够进行关联和学习。从历史上看，统计物理学和神经科学在人工神经网络的创立和早期发展中都发挥了开创性作用。McCulloch 和 Pitts 在1943年为生物神经网络建模首次引入线性-非线性人工神经元以及神经元之间的突触权重[49]，这至今仍是现代深度学习神经网络的基本构建块。统计物理学在80年代末和90年代人工神经网络的初期发展和理论理解中也发挥了重要作用，推动了诸多关键发展，包括 Hopfield 模型 [14]、玻尔兹曼机 [9] 以及自旋玻璃 （spin-glass） 理论的神经网络应用[50]等。

现在有什么不同？在基本层面上，没有太大变化，McCulloch–Pitts 神经元仍然是所有深度学习算法的基本构建块，线性求和与非线性激活仍然是单个神经元层面的基本计算过程。然而，规模却有着巨大的差异。正如在前面蛋白质折叠背景中所讨论的，我们现在拥有海量数据来训练大型人工神经网络模型；反过来，这些模型可以通过使用大量参数来吸收大型数据集中的信息。这些大模型的架构比 Rosenblatt 的原始感知器模型[51]复杂得多，例如，对现代大语言模型 （large language model， LLM） 来说 transformer 架构至关重要。当然，这些大型人工神经网络的性能远远超出了我们基于观察单个神经元所形成的预期。

这让我们想起 P. W. 安德森 （Anderson） 的著名论断：“多者异也” （More is different） [52]，他提出整个系统不仅仅是其各个部分的总和，系统中各个部分的相互作用可以产生涌现 （不同的） 行为。安德森这句名言激励了几代物理学家研究复杂多体系统的涌现行为，我们也想用它作为口号，号召物理学家们来研究出现在 （有时） 庞大但始终具有良好结构的人工神经网络中的迷人涌现行为——学习（learning） 。这些研究需要回答一些普遍性问题：学习如何从神经元相互作用中产生，深度学习神经网络究竟学到了什么，以及它们是否能够泛化所学到的知识。

确实，我们认为深度学习的下一个突破可能来自于基于统计物理学概念和方法建立的坚实理论基础。这将与不断推出的更先进的深度学习神经网络算法相辅相成，这些算法将加快物理和生物世界的科学发现步伐。这两个相互关联的新兴研究主题——基础理论和复杂应用——将极大地推进科学和人工智能技术的发展。在下文中，我们将在深入探讨几个可能取得进展的有前景的方向之前，先介绍描述机器学习过程的一般框架。我们的讨论将简要概述本特刊中与这些方向相关的已发表论文。

3.1 机器学习的中心法则

在 Ambrose 等人[53]所著的《学习如何运作？》 （How learning works?） 一书中，学习被定义为“一个导致变化的过程，这种变化源于经验，并增加了提高未来表现和学习能力的潜力”。虽然这本书是在人类 （学生） 学习的背景下写成的，但这个简明的学习定义同样可以用来描述机器学习。在图2中，我们展示了机器学习 （如基于神经网络的深度学习） 的关键组成部分和工作流程，我们称之为机器学习的“中心法则”。机器学习过程的目标是学习一个能够捕捉观测数据所代表的外部世界内在属性的模型。该模型具有特定的结构，即函数形式，并由其参数 （在神经网络模型中称为权重） 来参数化。遵循 Ambrose 等人给出的定义，在学习过程的训练阶段，模型中的参数会发生变化，这种变化源于对经验 （或者机器学习所说的训练数据） 的训练。一旦经过训练，我们可以通过训练后模型在未见过的测试数据上的表现，以及训练后模型是否为未来学习形成了良好的基础 （起点） 来评估其学习质量。

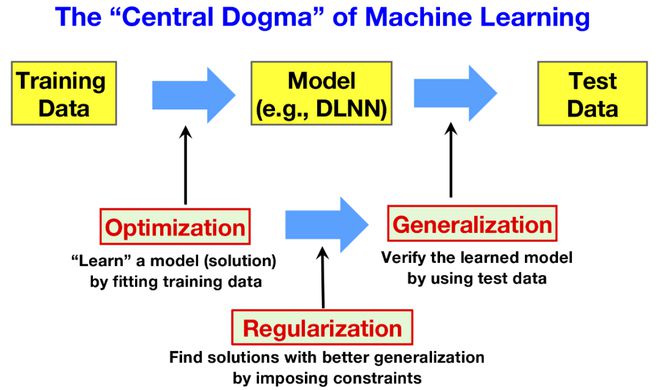
图2. 机器学习中主要步骤和工作流程的说明。用红色突出显示的是可能通过基于物理的方法解决的三个方向。

图2所示的机器学习工作流程立即提示了机器学习中的两个重要问题。第一个问题关注学习动力学（learning dynamics） 。具体来说，给定训练数据时，模型的参数如何变化？通常的学习过程是通过最小化损失函数来进行的，损失函数刻画了模型对训练数据的拟合程度。从一组初始参数值开始，参数在损失函数的指导下在高维参数空间中迭代更新，直到达到最小值。模型在这样的最小值处的参数构成了问题的一个解。优化过程，即参数更新序列，可以被视为以更新步为时间的学习动力学。第二个问题处理泛化问题。通常，深度学习神经网络是过参数化的。因此，拟合训练数据这一问题有许多可能的解 （最小值） 。问题在于哪个解具有更好的泛化性，即在训练过程未使用的测试数据上表现更好。如果我们知道什么类型的解具有更好的泛化能力，一个相关的问题是我们可以使用什么正则化项 （除了损失函数之外） 来推动系统朝着那些更具可泛化性的解发展。在接下来的两节中，我们将更详细地深入探讨这两个一般性问题，并强调这些方向上的一些最新发展。

3.2 随机学习动力学：从涨落的损失景观上滚落

人工神经网络中的一般优化策略包括通过跟随损失函数的梯度来更新权重，这种方法称为梯度下降 （gradient descent，GD） 。鉴于深度学习神经网络的前馈架构，梯度下降可以通过反向传播 （backpropagation） 高效实现。然而，如果使用在所有训练数据上取平均的损失函数，梯度下降对大型数据集来说在计算上将是不可行的。为了规避大数据集问题，可利用随机梯度下降（stochastic gradient descent，SGD） 方法代替梯度下降，该方法在每次迭代时会随机选择一个样本子集 （小批量） ，并用其更新权重 [54, 55]。值得注意的是，随后人们发现随机梯度下降对于在深度学习神经网络中找到更具泛化能力的解同样至关重要。

然而，尽管深度学习取得了巨大成功，但我们仍未充分理解，随机梯度下降为什么能在高维非凸损失函数 （能量） 景观中有效地学到好的解决方案。随机性似乎是随机梯度下降的关键，但这也使其更难理解。幸运的是，许多物理和生物系统都包含这样的随机元素，例如布朗运动和随机生化反应。并且我们已经开发出了强大的工具，来理解具有多个自由度的随机系统中的集体行为。事实上，统计物理学和随机动力系统理论中的概念和方法最近已被用于研究深度学习神经网络中的随机梯度下降动力学、损失函数景观及它们之间的关系。

为了展示这种基于物理学的方法在理解深度学习神经网络方面的实用性，我们简要描述一个研究随机梯度下降学习动力学的理论框架，及从中获得的一些有趣见解。我们首先将基于随机梯度下降的学习过程视为一个随机动力系统。像神经网络 （neural network，NN） 特别是深度神经网络 （deep neural network，DNN） 这样的学习系统具有大量（N）的权重参数wi（1, 2, …, N）。对于监督学习 （supervised learning） ，我们有M个训练样本，每个样本都有一个输入和一个正确输出，其中k = 1, 2, ..., M。对于每个输入，学习系统会预测一个输出，其中输出函数G取决于神经网络的架构和其权重。学习的目标是找到权重参数以最小化预测输出和正确输出之间的差异，这种差异由整体损失函数 （或能量函数） 刻画：

其中d(, )是和之间的距离度量。这里，一个典型的距离度量是交叉熵。

具体来说，随机梯度下降中第t次迭代的权重wi（1, 2, ..., N）的变化由下式给出：

其中 α 是学习率，μ(t)表示第t次迭代使用的随机小批量。大小为B的小批量μ的小批量损失函数 （minibatch loss function， MLF） 定义为：

其中μl标记随机选择的B个样本。

在这里，我们引入小批量损失函数系综 （ensemble） 这个关键概念，即一个能量景观的系综，每个景观来自于一个随机小批量。整体损失函数只是小批量损失函数的系综平均：。随机梯度下降噪声来自小批量损失函数与其系综平均之间的变化：。通过采用连续时间近似并保留方程（2）中的一阶时间导数项，我们得到随机梯度下降的随机偏微分方程如下：

其中时间t和本研究中的所有时间尺度都以小批量迭代时间Δt=1为单位来度量。连续时间极限相当于考虑远大于Δ的时间尺度，例如，一轮 （epoch） 的时间是M/B(>>1)。方程（4）类似于统计物理学中的朗之万方程 （Langevin equation） 。第一项是由整体损失函数L支配的确定性梯度下降，类似于物理学中的能量函数。第二项是随机梯度下降噪声项，其均值为零，等时协方差矩阵为

该矩阵明确依赖于，其给出了一种复杂形式的乘性噪声。对于给定的网络架构，学习动力学因此可以映射为一个“学习粒子”的随机运动，该粒子的坐标是网络的权重。特别地，随机梯度下降学习算法对应于学习粒子在涨落的能量景观中的下降过程，其由朗之万方程 （方程2） 支配，包含一个确定性梯度下降项和一个噪声项，其中噪声项的协方差矩阵由方程5给出。

随机梯度下降学习动力学中最不寻常和最有趣的部分来自噪声项。正如 Chaudhauri 和 Soatto [56]首次指出的，与平衡物理系统中噪声强度由热温度给定的情况不同，随机梯度下降动力学是高度非平衡的，因为随机梯度下降噪声既不是各向同性的也不是均匀的。从其定义来看，随机梯度下降噪声依赖于损失景观本身。其中最有趣的一个发现是随机梯度下降噪声的协方差矩阵与损失函数的 Hessian 矩阵高度相关：它们的特征方向高度对齐，且相应的特征值高度相关 [57, 58]。特别是，在损失景观中较陡峭的方向上 （Hessian 矩阵中较大的特征值） ，随机梯度下降噪声也更大。这导致在所有方向上权重方差与损失景观平坦度之间存在稳健的反比关系，这与平衡统计物理学中的涨落-响应关系 （fluctuation–response relation，又称爱因斯坦关系） 相反。

越来越多的经验证据支持这样一个观点：“好的” （可泛化的） 解存在于损失函数的平坦 （浅） 极小值处 [59-65]；然而，对于基于随机梯度下降的算法如何在高维权重空间中找到这些平坦极小值，我们仍然知之甚少。在随机学习动力学框架内获得的“反爱因斯坦关系”[57]表明，随机梯度下降充当了一个依赖于景观的退火算法。随机梯度下降的有效温度随着景观平坦度而降低，因此系统倾向于寻找平坦的极小值而非尖锐的极小值。正如最近一篇使用福克-普朗克方程 （Fokker-Planck equation） 研究随机梯度下降学习动力学权重分布的论文[58]所示，随机梯度下降在有效损失函数中引入了一个依赖于平坦度的项，该项使系统倾向于更平坦的极小值。

人工神经网络模型中的一个重要类别是生成模型，它们能够通过对现有样本的训练来生成新的样本。一个著名的早期例子是生成对抗网络 （generative adversarial network，GAN） 模型 [66]，已经有工作使用随机动力系统方法对其学习动力学进行了研究 [67]。事实上，一些最成功的生成模型，如基于扩散的模型[68]，都起源于物理学，并因此为基于物理学的研究提供了广阔空间。在本特刊中，Zdeborova 等人[69]从自旋玻璃的视角对不同生成模型进行了全面比较，这为理解这些强大生成模型的能力和局限性提供了理论见解。

3.3 泛化：高维的祝福与诅咒

物理学中的大多数问题都是过度约束的（或欠参数化的）。例如，在一个具有N个氨基酸的蛋白质折叠问题中，即使我们只考虑成对的相互作用能量，也有~N2个约束，远高于~2N个自由度 （即一维链上氨基酸的独立坐标） 。通常，一个过度约束的问题具有唯一解。这种情况如图3A所示，其中能量景观具有唯一的最小值，对应于折叠蛋白质的天然结构。通过最小化整体能量函数来解决过度约束的问题，例如从头算起的蛋白质折叠问题是一个众所周知的难题。另一方面，深度学习神经网络是过参数化的。参数 （权重） 的数量远大于数据中的内部自由度。深度学习神经网络中拥有大量参数的优势在于它使找到解 （损失景观中的最小值） 相对容易。然而，参数空间高维性的诅咒在于存在许多解 （损失函数的最小值） ，如图3B所示。因此，重要的问题变成了哪一个解对测试数据表现更好，即哪个解具有更好的泛化能力。

图3. 过度约束和约束不足问题中景观和解的差异。（A）蛋白质折叠（一个过度约束的问题）中的自由能景观，其中存在一个唯一的全局最小值，这通常很难找到。该图片采用自 Dill 和 Maccallum [70]。（B）过参数化（约束不足）深度学习模型中的损失景观，其可以具有多个全局最小值。挑战在于找出哪个解具有更好的泛化能力。

确实，泛化是机器学习中最重要的问题之一。考虑到深度学习神经网络中使用的庞大参数 （权重） 数量，这个问题变得更加紧迫。已经有很多工作基于各种理论和实证驱动的复杂度度量 （VC维、参数范数、锐度（sharpness）、路径范数等） 对深度学习神经网络的泛化性进行了研究。正如 Jiang 等 [71] 在最近的综述中总结的那样，经验证据表明基于锐度的度量与泛化之间存在强相关性 [72]，而许多其他 （理论驱动的） 度量，如基于范数的度量，并不能作为泛化的可靠指标 [71]。即使对于基于锐度的度量，我们也不理解它们为什么以及如何在预测泛化方面有效。此外，基于 Dinh 等人 [73] 指出的深度学习神经网络中的一般标度不变性，最近有研究工作对仅使用损失景观锐度来确定泛化的有效性提出了质疑。确实，对深度学习神经网络中泛化的全面理解仍然难以捉摸。

泛化中的一个关键问题是确定解的哪些性质决定了其泛化能力。回答这个问题的困难在于，虽然学习是由训练损失引导的，但泛化性能是由测试损失评估的，而在无法获取测试损失景观的情况下很难取得理论进展。最近，有工作通过使用数据变化和权重参数变化之间的等价性 （对偶性） 来解决这个问题 [74]。一般思路是，如果训练数据（x）和测试数据（x'）之间的输入变化等价于从解的权重（W）到新权重（W'）的变化，我们就可以使用这种对偶关系将输入空间中的分布映射到权重空间中，在那里我们可以评估泛化损失。值得注意的是，在任意密集连接层 （densely connected layer） 中都能找到这种精确对偶关系的无限族。通过使用具有最小权重变化的“最小”对偶关系，泛化损失可以被分解为权重空间中解的损失函数 Hessian 矩阵的不同特征方向上的贡献。这些贡献的形式揭示了泛化的两个不同决定因素——一个由损失景观的锐度支配，另一个对应于由训练数据和测试数据之间相对差异的协方差加权的解范数。从这项研究获得的主要见解之一是，泛化由这两个决定因素的乘积决定，这解决了 Dinh 等人[73]提出的关于平坦度的困惑。

在约束不足 （或过参数化） 的学习系统 （如深度学习神经网络） 中，正则化（regularization） 是添加到损失函数中的一个重要组成部分，目的是将系统推向具有更高泛化能力的解。然而，尽管正则化很重要，但它们通常是基于对更具泛化能力的解应具有什么特性的一些直觉。从影响泛化损失的两个贡献因素 （锐度和大小） 的角度来看，随机梯度下降和权重衰减作为两种有效正则化方案的能力背后的机制变得清晰。显然，基于底层系统的特性 （例如物理系统中的对称性和守恒定律） 和/或影响解的泛化能力的某些一般因素来设计正则化方案，将成为一个有趣的未来研究方向。

作为过拟合的极端情况，深度学习神经网络甚至可以“记忆”所有训练样本，即使它们的标签被替换为纯噪声[75]。这种过拟合 （记忆化） 解没有泛化能力。值得注意的是，深度学习神经网络避免了过拟合，其测试误差遵循所谓的“双下降” （double descent） 曲线[76]。随着模型容量 （复杂度） 的增加，测试误差在开始时遵循常规的 U 形曲线，先下降，然后在模型达到零训练误差时的插值阈值附近达到峰值。然而，当模型容量超过这个插值阈值时，它再次下降，测试误差在过参数化区域 （参数数量远大于样本数量） 达到其 （全局） 最小值。通过使用简单模型，人们在理解这种双下降行为方面取得了快速进展。例如，对于过参数化的简单两层网络，在线性可分数据上使用带泄漏的 ReLU 激活函数时，已有工作证明了优化和泛化性得以确保 [77]。这一结果随后被扩展到使用 ReLU 激活函数的2层网络 [78] 和使用平滑激活函数的2&3层网络[79]。神经正切核 （Neural Tangent Kernel，NTK） [80] 将大型 （宽） 神经网络与核方法联系了起来，使用 NTK 的方法表明，在过参数化区域，泛化误差以幂律方式 （其中Np为参数数量） 向平台值下降 [81]。在简单的合成学习模型 （synthetic learning models） 中，如具有岭回归 （ridge regression） 损失函数的随机特征模型，双下降行为已经得到解析证明 [82]。这一解析结果已经通过使用副本方法 （replica method） 扩展到其他合成学习模型 （例如随机流形模型） 和更一般的损失函数 [83]。

事实上，在大语言模型等大模型中，最令人兴奋的实证发现之一是，当模型规模和数据规模按比例一起增加时，泛化损失会随着它们的增加而持续下降，呈现出明显的幂律依赖关系。物理学家很自然地被幂律所描述的行为吸引，并开发出重整化群理论等强大工具来解释临界现象中的标度律 （scaling law） 。因此，我们认为理解大型复杂学习系统中泛化对数据规模和模型规模的“幂律”依赖关系，是对物理学家最具吸引力且极其重要的研究方向之一。在本特刊中，Bahri 等人 [84] 研究了这种“标度律”背后可能的起源，并为不同的标度区域提供了一个分类法。

3.4 真实神经网络和真实神经元的启发

如我们上述所言，人工神经网络受益于两个自然科学学科，即神经科学和统计物理学。然而，除了体现在 McCulloch–Pitts 神经元和分层前馈神经网络 （感知器） 架构中的最初神经科学启发之外，深度学习神经网络并没有包含太多神经科学的见解。尽管本特刊主要关注物理学和机器学习之间的交叉对话，但我们对神经科学产生的新概念的需求比以往任何时候都更大。深度学习神经网络的几个具体架构限制方面可能会从更深入的神经科学原理中受益。例如，深度学习的成功主要局限于具有静态数据集的静态任务，而且还需要大量明确标记的数据。由于许多研究人员已经注意到生物大脑极其适应动态环境中的动态任务，我们认为更好地理解大脑如何执行动态任务将带来新的概念，从而推动机器学习在此类任务上性能的提高。通过探索真实大脑计算与深度学习神经网络算法和架构之间的主要差异，可能会产生新的脑启发的算法。在本特刊中， Haim Sompolinksy 等人[85] 从表征和泛化的角度对人工神经网络和大脑神经网络进行了新颖的观点阐述和深入比较。

除了表征和泛化之外，我们列出人工网络和大脑网络的另外两个差异，希望能够激发未来的工作，因为它们都可以用前面章节概述的基于物理学的方法进行研究：

• 大脑使用局部学习规则并且很少受监督。首先，深度学习神经网络主要关注监督学习，即对给定输入模式有明确标注正确输出的情况，而大脑似乎很少进行监督学习。相反，理论和实验数据表明，神经学习主要采用无监督学习（unsupervised learning）、时间预测性学习（temporal-predictive learning）和强化学习（reinforcement learning，RL）技术。在算法层面，深度学习神经网络的学习通过反向传播实现，这是一个全局学习规则，而大脑中的学习是通过赫布规则（Hebbian rule）等局部学习规则实现的。

   

• 大脑具有高度动态性并持续与环境互动。大多数深度学习神经网络使用静态前馈架构，或者具有导向稳态的弛豫特性。相比之下，大脑表现出复杂的动态行为 （例如，不同的大脑节律/振荡） ，这是由大量循环连接实现的。此外，当前的深度学习神经网络几乎完全致力于静态的纯感知任务，而大脑的首要目的是在与环境的持续感知-行动循环中产生行为。

   

如本特刊中 Chklovskii 等人[86]所述，从神经科学获得的新启发也可以来自单个神经元层面。作者们引入概念将神经元作为其环境反馈的控制器，这是远超传统 McCulloch–Pitts 神经元的功能。这种创新方法不仅解释了此前看似无关的各种实验发现，还可能为创建更复杂的、受生物启发的人工智能系统指明方向。

参考文献

1. J. Jumper et al., Highly accurate protein structure prediction with alphafold. Nature 596, 583–589 (2021).

2. K. A. Dill, J. L. MacCallum, The protein-folding problem, 50 years on. Science 338, 1042–1046 (2012).

3. C. M. Dobson, Protein folding and misfolding. Nature 426, 884–890 (2003).

4. J. N. Onuchic, P. G. Wolynes, Theory of protein folding. Curr. Opin. Struct. Biol. 14, 70–75 (2004).

5. M. K. Higgins, Can we alphafold our way out of the next pandemic? J. Mol. Biol. 433, 167093 (2021).

6. H. Park, P. Patel, R. Haas, E. Huerta, APACE: Alphafold2 and advanced computing as a service for accelerated discovery in biophysics. Proc. Natl. Acad. Sci. U.S.A. 121, e2311888121 (2024).

7. N. Qian, T. J. Sejnowski, Predicting the secondary structure of globular proteins using neural network models. J. Mol. Biol. 202, 865–884 (1988).

8. M. Minsky, S. A. Papert, Perceptrons, Reissue of the 1988 Expanded Edition with a New Foreword by Léon Bottou: An Introduction to Computational Geometry (MIT Press, 2017).

9. D. H. Ackley, G. E. Hinton, T. J. Sejnowski, A learning algorithm for Boltzmann machines. Cognit. Sci. 9, 147–169 (1985).

10. D. E. Rumelhart, J. L. McClelland, Corporate PDP Research Group, Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations (MIT Press, 1986).

11. Y. LeCun, L. Bottou, Y. Bengio, P. Haffner, Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998).

12. P. Baldi, “Autoencoders, unsupervised learning, and deep architectures” in Proceedings of ICML Workshop on Unsupervised and Transfer Learning (JMLR Workshop and Conference Proceedings, 2012), pp. 37–49.

13. J. Gui, Z. Sun, Y. Wen, D. Tao, J. Ye, A review on generative adversarial networks: Algorithms, theory, and applications. IEEE Trans. Knowl. Data Eng. 35, 3313–3332 (2021).

14. J. J. Hopfield, Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. U.S.A. 79, 2554–2558 (1982).

15. J. Martin, M. Lequerica-Mateos, J. Onuchic, I. Coluzza, F. Morcoc, Machine learning in biological physics: From biomolecular prediction to design. Proc. Natl. Acad. Sci. U.S.A. 121, e2311807121 (2024).

16. Protein data bank, The single global archive for 3D macromolecular structure data. Nucleic Acids Res. 47, D520–D528 (2019).

17. J. I. Sułkowska, F. Morcos, M. Weigt, T. Hwa, J. N. Onuchic, Genomics-aided structure prediction. Proc. Natl. Acad. Sci. U.S.A. 109, 10340–10345 (2012).

18. D. De Juan, F. Pazos, A. Valencia, Emerging methods in protein co-evolution. Nat. Rev. Genet. 14, 249–261 (2013).

19. A. Davtyan et al., AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J. Phys. Chem. B 116, 8494–8503 (2012).

20. J. D. Bryngelson, P. G. Wolynes, Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. U.S.A. 84, 7524–7528 (1987).

21. J. D. Bryngelson, J. N. Onuchic, N. D. Socci, P. G. Wolynes, Funnels, pathways, and the energy landscape of protein folding: A synthesis. Prot.: Struct. Funct. Bioinf. 21, 167–195 (1995).

22. S. Yang et al., Domain swapping is a consequence of minimal frustration. Proc. Natl. Acad. Sci. U.S.A. 101, 13786–13791 (2004).

23. R. D. Hills Jr, C. L. Brooks III, Insights from coarse-grained g ̄o models for protein folding and dynamics. Int. J. Mol. Sci. 10, 889–905 (2009).

24. S. Tripathi, D. A. Kessler, H. Levine, Biological networks regulating cell fate choice are minimally frustrated. Phys. Rev. Lett. 125, 088101 (2020).

25. K. M. Ruff, R. V. Pappu, Alphafold and implications for intrinsically disordered proteins. J. Mol. Biol. 433, 167208 (2021).

26. M. Di Pierro, B. Zhang, E. L. Aiden, P. G. Wolynes, J. N. Onuchic, Transferable model for chromosome architecture. Proc. Natl. Acad. Sci. U.S.A. 113, 12168–12173 (2016).

27. M. A. Marti-Renom, L. A. Mirny, Bridging the resolution gap in structural modeling of 3D genome organization. PLoS Comput. Biol. 7, e1002125 (2011).

28. U. Lupo, D. Sgarbossa, A. F. Bitbol, Pairing interacting protein sequences using masked language modeling. Proc. Natl. Acad. Sci. U.S.A. 121, e2311887121 (2024).

29. B. Meynard-Piganeau, C. Feinauer, M. Weigt, A. M. Walczak, T. Mora, Tulip-a transformer based unsupervised language model for interacting peptides and T-cell receptors that generalizes to unseen epitopes. bioRxiv [Preprint] (2023). https://www.biorxiv.org/content/10.1101/2023.07.19.549669v1 (Accessed 10 January 2024).

30. B. P. Kwee et al., STAPLER: Efficient learning of TCR-peptide specificity prediction from full-length TCR-peptide data. bioRxiv [Preprint] (2023). https://www.biorxiv.org/content/10.1101/2023.04.25.538237v1 (Accessed 10 January 2024).

31. A. T. Wang et al., RACER-m leverages structural features for sparse T cell specificity prediction. bioRxiv [Preprint] (2023). https://www.biorxiv.org/content/10.1101/2023.08.06.552190v1 (Accessed 3 January 2024).

32. B. A. Camley, W. J. Rappel, Physical models of collective cell motility: From cell to tissue. J. Phys. D: Appl. Phys. 50, 113002 (2017).

33. M. Basan, J. Elgeti, E. Hannezo, W. J. Rappel, H. Levine, Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing. Proc. Natl. Acad. Sci. U.S.A. 110, 2452–2459 (2013).

34. V. Hakim, P. Silberzan, Collective cell migration: A physics perspective. Rep. Progr. Phys. 80, 076601 (2017).

35. J. LaChance, K. Suh, J. Clausen, D. J. Cohen, Learning the rules of collective cell migration using deep attention networks. PLoS Comput. Biol. 18, e1009293 (2022).

36. S. U. Hirway, S. H. Weinberg, A review of computational modeling, machine learning and image analysis in cancer metastasis dynamics. Comput. Syst. Oncol. 3, e1044 (2023).

37. S. Al-Janabi, A. Huisman, P. J. Van Diest, Digital pathology: Current status and future perspectives. Histopathology 61, 1–9 (2012).

38. D. B. Brückner et al., Stochastic nonlinear dynamics of confined cell migration in two-state systems. Nat. Phys. 15, 595–601 (2019).

39. R. Yu, R. Wang, Learning dynamical systems from data: An introduction to physics-guided deep learning. Proc. Natl. Acad. Sci. U.S.A. 121, e2311808121 (2024).

40. D. Kochkov et al., Machine learning-accelerated computational fluid dynamics. Proc. Natl. Acad. Sci. U.S.A. 118, e2101784118 (2021).

41. E. M. King, C. X. Du, Q.-Z. Zhu, S. S. Schoenholz, M. P. Brenner, Programming patchy particles for materials assembly design. Proc. Natl. Acad. Sci. U.S.A. 121, e2311891121 (2024).

42. R. E. Wengert, A simple automatic derivative evaluation program. Commun. ACM 7, 463–464 (1964).

43. F. Ruehle, Data science applications to string theory. Phys. Rep. 839, 1–117 (2020).

44. Y. LeCun, Y. Bengio, G. Hinton, Deep learning. Nature 521, 436 EP (2015).

45. I. Goodfellow, A. Courville, Y. Bengio, Deep Learning (MIT Press, 2016), vol. 1.

46. K. He, X. Zhang, S. Ren, J. Sun, “Deep residual learning for image recognition” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2016), pp. 770–778.

47. Y. Wu et al., Google’s neural machine translation system: Bridging the gap between human and machine translation. arXiv [Preprint] (2016). http://arxiv.org/abs/1609.08144 (Accessed 3 January 2024).

48. D. Silver et al., Mastering the game of go with deep neural networks and tree search. Nature 529, 484–489 (2016).

49. W. Mcculloch, W. Pitts, A logical calculus of ideas immanent in nervous activity. Bull. Math. Biophys. 5, 127–147 (1943).

50. D. J. Amit, H. Gutfreund, H. Sompolinsky, Spin-glass models of neural networks. Phys. Rev. A 32, 1007 (1985).

51. F. Rosenblatt, The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 65, 386–408 (1958).

52. P. W. Anderson, More is different. Science 177, 393–396 (1972).

53. S. Ambrose, M. Bridges, M. Lovett, How Learning Works: 7 Research-Based Principles for Smart Teaching (John Wiley and Sons, San Francisco, 2010).

54. H. Robbins, S. Monro, A stochastic approximation method. Ann. Math. Stat. 22, 400–407 (1951).

55. L. Bottou, “Large-scale machine learning with stochastic gradient descent” in Proceedings of COMPSTAT 2010, Y. Lechevallier, G. Saporta Eds. (Physica-Verlag HD, Heidelberg, 2010), pp. 177–186.

56. P. Chaudhari, S. Soatto, “Stochastic gradient descent performs variational inference, converges to limit cycles for deep networks” in 2018 Information Theory and Applications Workshop (ITA) (2018). http://dx.doi.org/10.1109/ita.2018.8503224.

57. Y. Feng, Y. Tu, The inverse variance-flatness relation in stochastic gradient descent is critical for finding flat minima. Proc. Natl. Acad. Sci. U.S.A. 118 (2021).

58. N. Yang, C. Tang, Y. Tu, Stochastic gradient descent introduces an effective landscape-dependent regularization favoring flat solutions. Phys. Rev. Lett. 130, 237101 (2023).

59. G. E. Hinton, D. van Camp, “Keeping the neural networks simple by minimizing the description length of the weights” in Proceedings of the Sixth Annual Conference on Computational Learning Theory, COLT 1993 (ACM, New York, NY, USA, 1993), pp. 5–13.

60. S. Hochreiter, J. Schmidhuber, Flat minima. Neural Comput. 9, 1–42 (1997).

61. C. Baldassi et al., Unreasonable effectiveness of learning neural networks: From accessible states and robust ensembles to basic algorithmic schemes. Proc. Natl. Acad. Sci. U.S.A. 113, E7655–E7662 (2016).

62. P. Chaudhari et al., Entropy-SGD: Biasing Gradient Descent into Wide Valleys (ICLR, 2017).

63. Y. Zhang, A. M. Saxe, M. S. Advani, A. A. Lee, Energy-entropy competition and the effectiveness of stochastic gradient descent in machine learning. Mol. Phys. 116, 3214–3223 (2018).

64. S. Mei, A. Montanari, P. M. Nguyen, A mean field view of the landscape of two-layer neural networks. Proc. Natl. Acad. Sci. U.S.A. 115, E7665–E7671 (2018).

65. C. Baldassi, F. Pittorino, R. Zecchina, Shaping the learning landscape in neural networks around wide flat minima. Proc. Natl. Acad. Sci. U.S.A. 117, 161–170 (2020).

66. I. Goodfellow et al., “Generative adversarial nets” in Advances in Neural Information Processing Systems, Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, K. Weinberger, Eds. (Curran Associates, Inc., 2014), vol. 27.

67. S. Durr, Y. Mroueh, Y. Tu, S. Wang, Effective dynamics of generative adversarial networks. Phys. Rev. X 13, 041004 (2023).

68. J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan, S. Ganguli, “Deep unsupervised learning using nonequilibrium thermodynamics” in Proceedings of the 32nd International Conference on Machine Learning, Proceedings of Machine Learning Research, F. Bach, D. Blei, Eds. (PMLR, Lille, France, 2015), vol. 37, pp. 2256–2265.

69. D. Ghioa, Y. Dandi, F. Krzakala, L. Zdeborova, Sampling with flows, diffusion and autoregressive neural networks from a spin-glass perspective. Proc. Natl. Acad. Sci. U.S.A. 121, e2311810121 (2024).

70. K. Dill, J. Maccallum, The Protein-Folding Problem, 50 Years on (Science New York, N.Y., 2012), vol. 338, pp. 1042–1046.

71. Y. Jiang, B. Neyshabur, H. Mobahi, D. Krishnan, S. Bengio, Fantastic generalization measures and where to find them. ICLR (2020).

72. N. S. Keskar, D. Mudigere, J. Nocedal, M. Smelyanskiy , P. T. P. Tang , On large-batch training for deep learning: Generalization gap and sharp minima. ICLR (2017).

73. L. Dinh, R. Pascanu, S. Bengio, Y. Bengio, “Sharp minima can generalize for deep nets” in Proceedings of 34th International Conference Machine Learning (2017), vol. 70, pp. 1019–1028.

74. Y. Feng, W. Zhang, Y. Tu, Activity-weight duality in feed-forward neural networks reveals two co-determinants for generalization. Nat. Mach. Intell. 5, 908–918 (2023).

75. C. Zhang, S. Bengio, M. Hardt, B. Recht, O. Vinyals, Understanding deep learning requires rethinking generalization. ICLR (2017).

76. M. Belkin, D. Hsu, S. Ma, S. Mandal, Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proc. Natl. Acad. Sci. U.S.A. 116, 15849–15854 (2019).

77. A. Brutzkus, A. Globerson, E. Malach , S. Shalev-Shwartz , SGD learns over-parameterized networks that provably generalize on linearly separable data. ICLR (2018).

78. Y. Li, Y. Liang, Learning overparameterized neural networks via stochastic gradient descent on structured data. Adv. Neural Inf. Process. Syst. 31, 8157–8166 (2018).

79. Z. Allen-Zhu, Y. Li, Z. Song, “A convergence theory for deep learning via over-parameterization” in International Conference Machine Learning (2019), pp. 242–252.

80. A. Jacot, F. Gabriel, C. Hongler, Neural tangent kernel: Convergence and generalization in neural networks. Adv. Neural Inf. Process. Syst. 31, 8571–8580 (2018).

81. M. Geiger et al., Scaling description of generalization with number of parameters in deep learning. J. Stat. Mech.: Theory Exp. 2020, 023401 (2020).

82. S. Mei, A. Montanari, The generalization error of random features regression: Precise asymptotics and the double descent curve. Commun. Pure Appl. Math. 75, 667–766 (2022).

83. F. Gerace, B. Loureiro, F. Krzakala, M. Mézard, L. Zdeborová, Generalisation error in learning with random features and the hidden manifold model (ICML, 2020), pp. 3452–3462.

84. Y. Bahri, E. Dyer, J. Kaplan, J. Lee, U. Sharma, Explaining neural scaling laws. Proc. Natl. Acad. Sci. 121, e2311878121 (2024).

85. Q. Li, B. Sorscher, H. Sompolinsky, Representations and generalization in artificial and brain neural networks. Proc. Natl. Acad. Sci. U.S.A. 121, e2311805121 (2024).

86. J. Moore et al., The neuron as a direct data-driven controller. Proc. Natl. Acad. Sci. U.S.A. 2023–11893 (2024).

转载请注明：可思数据 » 物理学遇见机器学习：深度学习的下一个突破可能来自统计物理学