1、一战成名

  2012年，一个代表人工智能技术转折的故事正在悄然上演。这个故事的主角是加拿大的多伦多大学计算机科学系教授Geoffrey Hinton，被誉为“神经网络之父”，以及他的两位学生：Alex Krizhevsky和 Ilya Sutskever。他们三人共同打造了一个名为AlexNet的深度神经网络模型，这个模型即将在当年的ImageNet挑战赛上大放异彩。2012年12月，ImageNet挑战赛上，AlexNet以其惊人的性能一骑绝尘，将图像分类的错误率降低了一半，以远超第二名的成绩拿到了比赛的冠军，这一成就震惊了整个人工智能领域，证明了深度神经网络的巨大潜力。这个胜利不仅仅是一个比赛的胜利，更是深度学习时代的开启。从上世纪的1956年在达特茅斯会议上首次提出“人工智能”这一概念，科学家就一直在探索能够模拟人类智能的算法和模型，为什么深度神经网络能够在众多的机器学习算法中脱颖而出呢？有学者认为深度神经网络理论上是一种广义上的“超级函数”，它能够模拟任何输入和输出。

2、函数

  函数是数学中最重要的概念之一，它代表的是变量之间的关系。1930 年新的现代函数定义为“若对集合M的任意元素x，总有集合 N确定的元素 y与之对应，则称在集合M 上定义一个函数，记为 f 。元素x 称为 自变量 ，元素 y 称为 因变量” 。这种函数关系可以表示为：y=f(x)。初中数学就有函数的相关知识，比如：二次函数的表达式为：

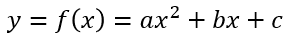
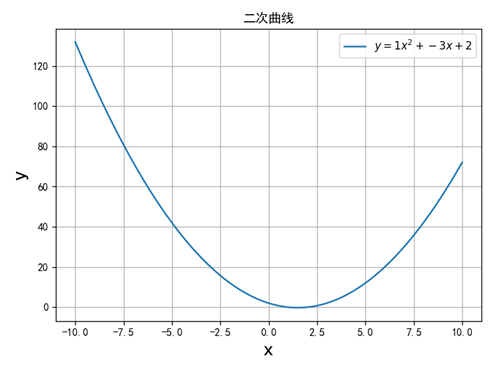
将该函数的取值x, y在笛卡尔坐标系中描绘出来，就是一条抛物线（如下图，a=1,b=-3,c=2）。如果将深度神经网络的输入和输出分别定义为自变量和因变量，那么就可以把它当作函数来研究。

3、超级函数

  首先，深度神经网络可以近似任何普通函数。例如，用正弦函数y=0.4sin⁡(x)产生30000个数据对(x,y)（下图中蓝色点），其中自变量x的变化范围为-9到9，因变量y的值加入了噪声（增加难度）。使用这些数据训练一个神经网络，图中红色的曲线为训练后神经网络近似结果。需要说明的是，这种近似函数，可以是单变量输入单变量输出，也可以是多变量输入多变量输出。

  其次，深度神经网络，可以实现任意多模态的输入和输出。比如，让深度神经网络学习识别猫和狗的图片。训练完成后，将猫或狗的图片作为输入，神经网络会输出猫或狗的标签，如下图：

也可以，输入一张工业产品图片，输出一张标明产品缺陷的图片，如下图：

也可以，输入蛋白质的生物大分子式，输出相应的三维结构，如下图：

为什么神经网络能够成为一个超级函数呢？还得回到神经网络本身，从它的结构找线索。

4、万能逼近定理

  计算机科学家已经从数学上严格证明了，多层神经网络可以模拟任意函数。下面，我们选择一个最简单的神经网络（如下图），通过计算它的前向传播过程，展现神经网络的内部机制。

实验网络分三层：输入层、隐藏层和输出层。输入层含一个输入变量x，中间层含三个神经元h1、h2、h3，输出层含一个输出变量y，神经网络的前向传播分四步。

第一步，输入层到隐藏层:

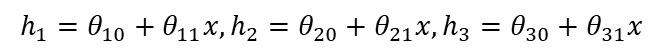
第二步，隐藏层激活：

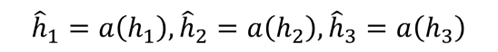
第三步，从隐藏层到输出：

第四步，输出：

综合前面的四个步骤，该神经网络的前向传播计算公式如下：

下面开始计算神经网络的前向传播，x在0到1之间取值，模型所有参数取值：

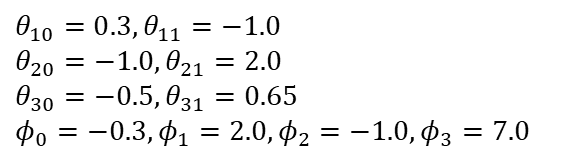
隐藏层激活函数公式和图像如下：

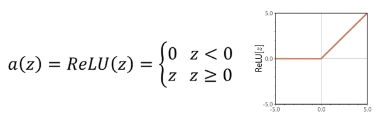
  计算结果如下图，左图中的上面三条曲线分别代表三个隐藏层神经元接收到的输入层传递过来的值（第一步），中间三条曲线分别代表通过隐藏层神经元激活后的值（第二步），下面三条曲线，为隐藏层传递到输出层的值（第三步），右图为最后的输出（第四步）。

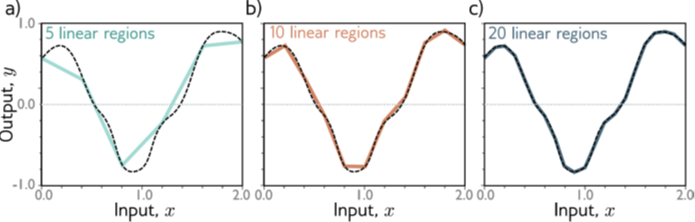
当我们用神经网络拟合函数时，隐藏层神经元越多，输出的曲线越光滑，拟合的精度也越高（下图）。

转载请注明：可思数据 » 深度神经网络：一种超级函数