LinUCB 浅析

这里只简单介绍一下 LinUCB 算法的流程，真的是浅析，浅析！

在推荐系统中，通常把待推荐的商品作为 MAB 问题的 arm。UCB 是 context-free 类的算法，没有充分利用推荐场景的上下文信息，为所有用户的选择展现商品的策略都是相同的，忽略了用户作为一个个活生生的个性本身的兴趣点、偏好、购买力等因素，因而，同一个商品在不同的用户、不同的情景下接受程度是不同的。故在实际的推荐系统中，context-free 的 MAB 算法基本都不会被采用。

与 context-free MAB 算法对应的是 Contextual Bandit 算法，顾名思义，这类算法在实现 E&E 时考虑了上下文信息，因而更加适合实际的个性化推荐场景。

在 LinUCB 中，每一个 arm 维护一组参数，用户和每一个 arm 的组合可以形成一个上下文特征（上下文特征的特征维度为 d），那么对于一个用户来说，在每个 arm 上所能够获得的期望收益如下：

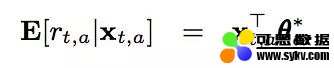
对于一个老虎机来说，假设收集到了 m 次反馈，特征向量可以写作 Da(维度为 m_d)，假设我们收到的反馈为 Ca(维度为 m_1)，那么通过求解下面的 loss，我们可以得到当前每个老虎机的参数的最优解：

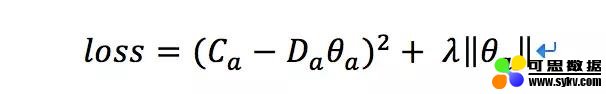
这其实就是岭回归嘛，我们很容易得到最优解为：

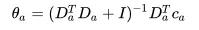
既然是 UCB 方法的扩展，我们除了得到期望值外，我们还需要一个置信上界，但是，我们没法继续用 Chernoff-Hoeffding Bound 的定理来量化这个上界，幸运的是，这个上界已经被人找到了：

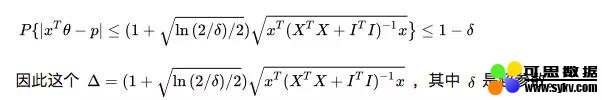
因此，我们推荐的 item 就能够确定了：

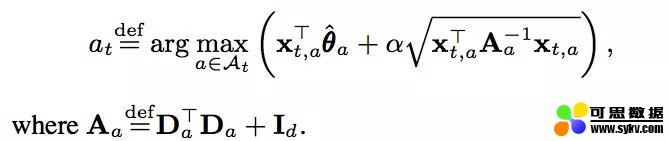
可以看到，我们在计算参数及最后推荐结果的时候，用到了以下几部分的信息：上下文特征 x，用户的反馈 c。而这些信息都是可以每次都存储下来的，因此在收集到了一定的信息之后，参数都可以动态更新，因此我们说 LinUCB 是一种在线学习方法。

什么是在线学习？个人简单的理解就是模型的训练和更新是在线进行的，能够实时的根据在线上的反馈更新模型的参数。

好了，我们来看一下 linUCB 算法的流程吧：

上面的 ba 可以理解为特征向量 x 和反馈 r 的乘积。

是否觉得一头雾水，不用着急，我们通过代码来一步步解析上面的流程。

本文地址：http://www.6aiq.com/article/1547825582955
本文版权归作者和AIQ共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出
知乎专栏点击关注

2、linUCB 代码实战

本文的代码地址为：https://github.com/princewen/tensorflow_practice/blob/master/recommendation/Basic-Bandit-Demo/Basic-LinUCB.py

设定超参数和矩阵

首先我们设定一些超参数，比如α，正反馈和负反馈的奖励程度 r1，r0，上下文特征的长度 d

self.alpha = 0.25
self.r1 = 0.6
self.r0 = -16
self.d = 6  # dimension of user features

接下来，我们设定我们的几个矩阵，比如 A 和 A 的逆矩阵，b(x 和 r 的乘积），以及参数矩阵：

self.Aa = {} # Aa : collection of matrix to compute disjoint part for each article a, d*d
self.AaI = {} # AaI : store the inverse of all Aa matrix

self.ba = {} # ba : collection of vectors to compute disjoin part, d*1
self.theta = {}

初始化矩阵

初始化矩阵对应上面的 4-7 步，A 设置为单位矩阵，b 设置为 0 矩阵，参数也设置为 0 矩阵，注意的是，每个 arm 都有这么一套矩阵：

def set_articles(self,art):
 for key in art:
 self.Aa[key] = np.identity(self.d) # 创建单位矩阵
 self.ba[key] = np.zeros((self.d,1))

 self.AaI[key] = np.identity(self.d)
 self.theta[key] = np.zeros((self.d,1))

计算推荐结果

计算推荐结果对应于上面的 8-11 步，我们直接根据公式计算当前的最优参数和置信上界，并选择最大的 arm 作为推荐结果。代码中有个小 trick，及对所有的 arm 来说，共同使用一个特征，而不是每一个 arm 单独使用不同的特征：

def recommend(self,timestamp,user_features,articles):
 xaT = np.array([user_features]) # d * 1
 xa = np.transpose(xaT)

 AaI_tmp = np.array([self.AaI[article] for article in articles])
 theta_tmp = np.array([self.theta[article] for article in articles])
 art_max = articles[np.argmax(np.dot(xaT,theta_tmp) + self.alpha * np.sqrt(np.dot(np.dot(xaT,AaI_tmp),xa)))]

 self.x = xa
 self.xT = xaT

 self.a_max = art_max
 return self.a_max

更新矩阵信息

这对应于上面的 12-13 步，根据选择的最优 arm，以及得到的用户反馈，我们更新 A 和 b 矩阵：

def update(self,reward):
 if reward == -1:
 pass
 elif reward == 1 or reward == 0:
 if reward == 1:
 r = self.r1
 else:
 r = self.r0

 self.Aa[self.a_max] += np.dot(self.x,self.xT)
 self.ba[self.a_max] += r * self.x
 self.AaI[self.a_max] = np.linalg.inv(self.Aa[self.a_max])
 self.theta[self.a_max] = np.dot(self.AaI[self.a_max],self.ba[self.a_max])

 else:
 # error

写到这里，本来应该就要结束了，可是脑子里又想到一个问题，为什么可以直接通过加法来更新 A 矩阵？其实是个很简单的问题，试着写出 A 矩阵中每个元素的计算公式来，问题就迎刃而解了！