神经网络-全连接层（3）

1. class SquareLoss:
2.     def forward(self, y, t):
3.         self.loss = y - t
4.         return np.sum(self.loss * self.loss) /  self.loss.shape[1] / 2
5.     def backward(self):
6.         return self.loss

       为了代码的简洁，我们在前向运算的时候就把一些后向计算的信息都保存起来，这样在后向计算的时候就能简单点。这样这个类就不能具备多线程的特性了，不过想支持多线程的功能还有别的办法。后面的全连接层也会采用同样的思路——前向为后向准备运算数据。

      上一节我们讲了1个例子，输入有2个元素，第一层有4个输出，第2层有1个输出。我们假设训练数据有N个，我们对所有相关的训练数据和参数做以下的约定：

• 所有的训练数据按列存储，也就是说如果把N个数据组成一个矩阵，那个矩阵的行等于数据特征的数目，矩阵的列等于N
• 线性部分的权值w由一个矩阵构成，它的行数为该层的输入个数，列数为该层的输出个数。如果该层的输入为2，输出为4，那么这个权值w的矩阵就是一个2*4的矩阵。
• 线性部分的权值b是一个行数等于输出个数，列数为1的矩阵。

      基于上面的规则，我们把上一节的例子以批量数据的形式画成了下面一张图：

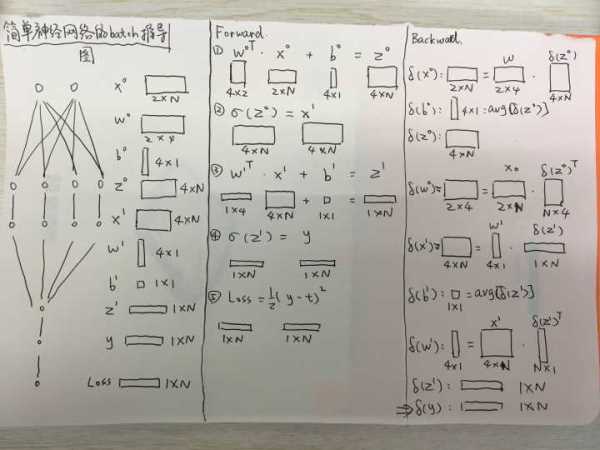
      这张图从左往右有三个部分：

• 最左边是神经网络的结构图，可以看出里面的数据x,z和参数w,b都符合我们刚才对数据组织的定义。
• 中间是神经网络前向的过程。一共分为5步，其中最后一步用来计算Loss。
• 最右边是神经网络反向的过程。这里需要仔细看一下。为了表达上的简洁，我们用残差符号\delta表达Loss对指定变量的偏导数。同时为了更加简洁地表达梯度计算的过程，在这个过程中我们对其中一个矩阵做了矩阵转置，这样可以确保最终输出维度的正确。

      对于上图右边的部分，需要认真地看几遍，最好能仔细地推导一遍，才能更好地掌握这个推导的过程，尤其是为了维度对矩阵做转置这部分。

      看懂了上面的图，接下来要做的就是对上面的内容进行总结，写出最终的矩阵版后向传播算法：

1. class FC:
2.     def __init__(self, in_num, out_num, lr = 0.1):
3.         self._in_num = in_num
4.         self._out_num = out_num
5.         self.w = np.random.randn(in_num, out_num)
6.         self.b = np.zeros((out_num, 1))
7.         self.lr = lr
8.     def _sigmoid(self, in_data):
9.         return 1 / (1 + np.exp(-in_data))
10.     def forward(self, in_data):
11.         self.topVal = self._sigmoid(np.dot(self.w.T, in_data) + self.b)
12.         self.bottomVal = in_data
13.         return self.topVal
14.     def backward(self, loss):
15.         residual_z = loss * self.topVal * (1 - self.topVal)
16.         grad_w = np.dot(self.bottomVal, residual_z.T)
17.         grad_b = np.sum(residual_z)
18.         self.w -= self.lr * grad_w
19.         self.b -= self.lr * grad_b
20.         residual_x = np.dot(self.w, residual_z)
21.         return residual_x

       好了，现在我们有了Loss类和全连接类，我们还需要一个类把上面两个类串联起来，这里为了后面的内容我们定义了许多默认变量：

1. class Net:
2.     def __init__(self, input_num=2, hidden_num=4, out_num=1, lr=0.1):
3.         self.fc1 = FC(input_num, hidden_num, lr)
4.         self.fc2 = FC(hidden_num, out_num, lr)
5.         self.loss = SquareLoss()
6.     def train(self, X, y): # X are arranged by col
7.         for i in range(10000):
8.             # forward step
9.             layer1out = self.fc1.forward(X)
10.             layer2out = self.fc2.forward(layer1out)
11.             loss = self.loss.forward(layer2out, y)
12.             # backward step
13.             layer2loss = self.loss.backward()
14.             layer1loss = self.fc2.backward(layer2loss)
15.             saliency = self.fc1.backward(layer1loss)
16.         layer1out = self.fc1.forward(X)
17.         layer2out = self.fc2.forward(layer1out)
18.         print 'X={0}'.format(X)
19.         print 't={0}'.format(y)
20.         print 'y={0}'.format(layer2out)

       代码是写完了，可是我们还需要验证一下自己的代码是不是正确的。一般来说我们会采用一些近似方法计算验证梯度是否正确。

      把我们的代码用博客上数据和结果做一下验证，就可以帮助我们修正代码做好debug。其实上面的代码本来也不多，可能犯错的地方也不多。

时间:2018-08-05 01:24  来源:    转发量:次