不平衡数据下的机器学习（下）

3.5 不平衡学习算法的实际应用效果对比

上面4小节已经给出了很多针对数据不平衡问题的处理算法，下面将对这些算法的实际应用效果进行对比，本节的所有数据与图表都来自于Buda, M.等人于2017年发表在Arxiv上的文章《A systematic study of the class imbalance problem in convolutional neural networks》。

 

 

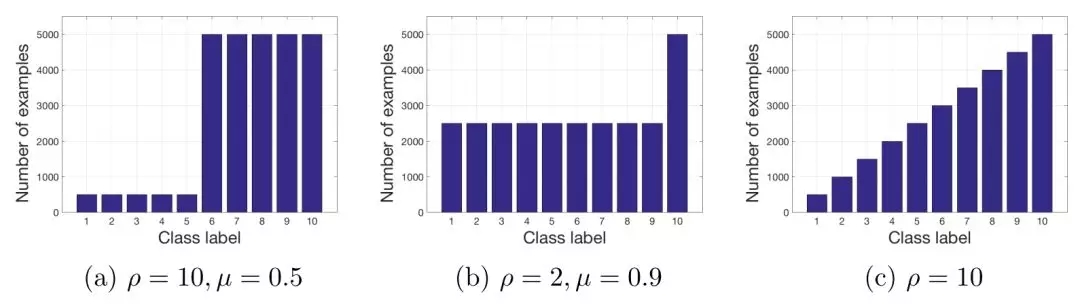
图 3.10 数据不平衡的形式。(a)和(b)为阶梯性不平衡，(c)为线性不平衡。

在这篇文章中，作者定义了2种数据不平衡的形式：阶梯性不平衡和线性不平衡，两种形式见图 3.10。评价指标为ROC AUC，实验了四种不平衡学习算法：

1)随机过采样

2)随机降采样

3)使用随机过采样方法预训练CNN模型，然后再使用原始数据集对模型最后一层做微调

4)使用随机降采样方法预训练CNN模型，然后再使用原始数据集对模型最后一层做微调

作者在MNIST、CIFAR-10和ImageNet这3个数据集上分别进行了实验，实验配置均在下表中列出：

 

 

3.5.1 在阶梯性不平衡数据上的实验结果

 

 

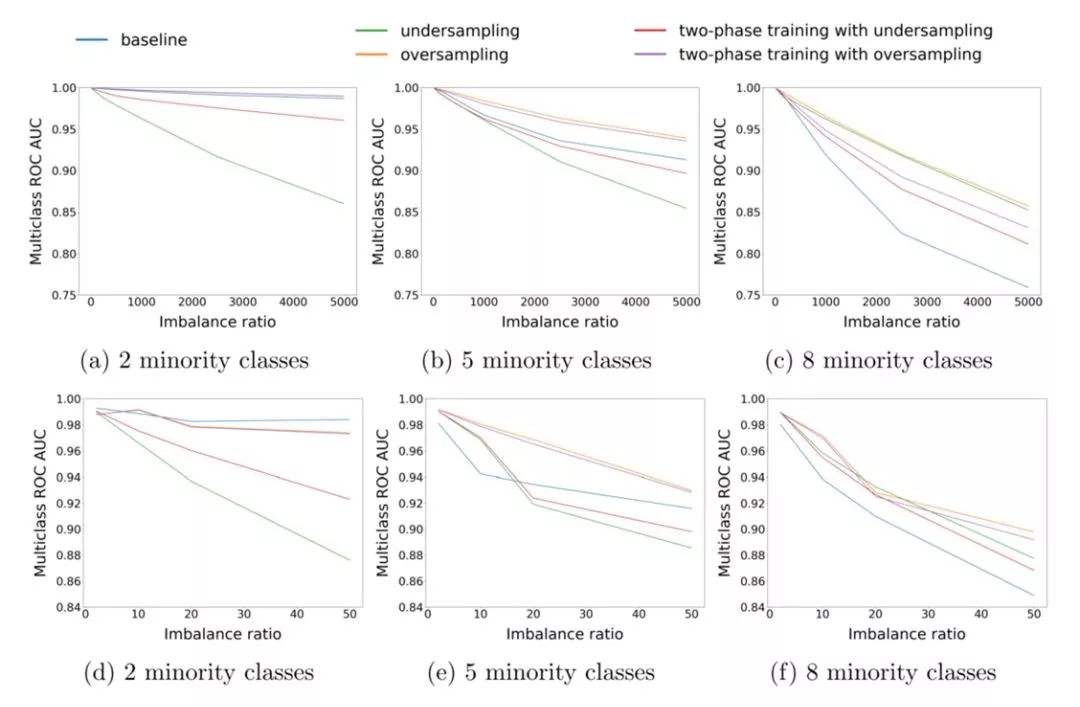
图 3.11 在阶梯状不平衡数据上，随不平衡比例变化的各个算法的表现。(a)(b)(c)为在MNIST上的结果，(d)(e)(f)为在CIFAR-10上的结果

从图 3.11中可以看到：相比于简单任务(MNIST)，数据不平衡对CNN在复杂任务(CIFAR-10)上的表现影响更大;随机过采样方法在几乎所有情况下都要优于其他方法。

 

 

图 3.12在阶梯状不平衡数据上，随少数类数量变化的各个算法的表现。(a)(b)(c)为在MNIST上的结果，(d)(e)(f)为在CIFAR-10上的结果

从图 3.12中也可以看出：使用随机过采样之后效果几乎始终优于原始的不使用任何不平衡学习算法的效果;预训练方法的效果始终介于非预训练方法和原始方法之间。

3.5.2 在线性不平衡数据上的实验结果

 

 

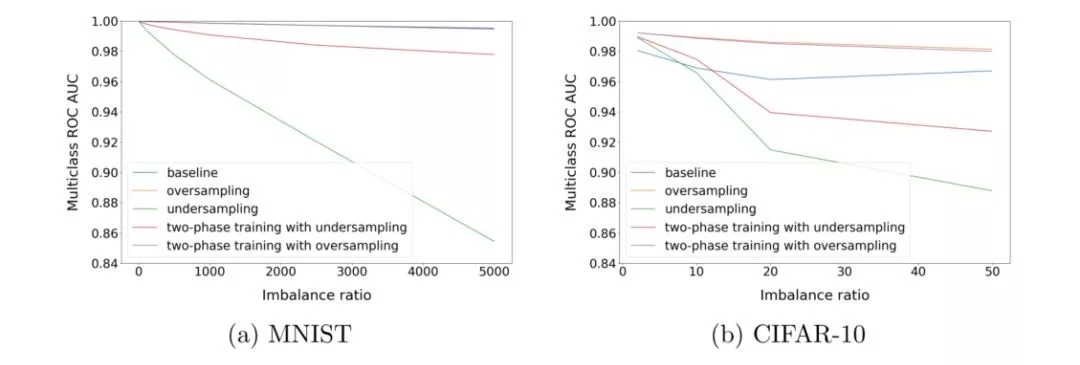
图 3.13 线性不平衡数据上的实验效果

从图 3.13可以看出：随机过采样对于实验效果始终有促进能力;随机降采样的效果则会随着不均衡比例的提升而逐渐下降。

 

 

上表给出了作者在ImageNet上的实验效果，可以看到，随机过采样方法还是始终优于随机降采样方法，但要差于不使用任何不平衡学习算法的Baseline方法。因为，我们在将采样方法应用于复杂任务时，需要格外小心。

3.5.4 过采样/降采样比例对实验结果的影响

 

 

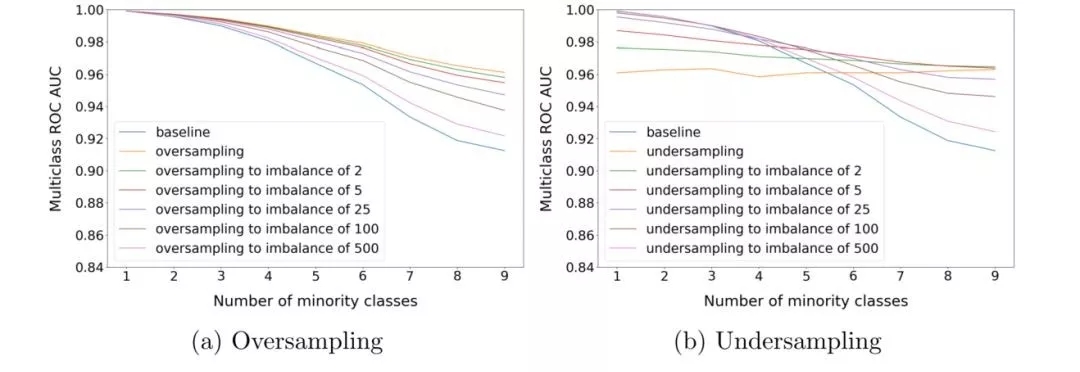
图 3.14 过采样/降采样比例对实验结果的影响

从图 3.14可以看到：随机过采样方法会在过采样到各类别完全均衡的情况下取得较好效果;随机降采样方法所需的较佳降采样比例则随着数据变化而变化。

3.5.5 对采样方法泛化能力的研究

 

 

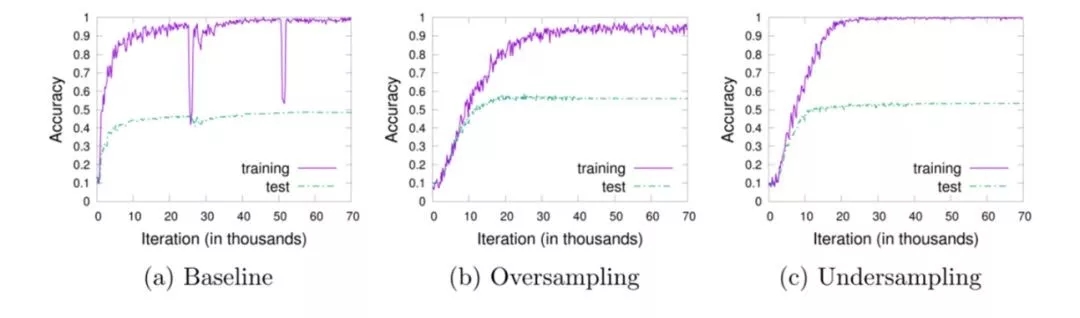
图 3.15 在CIFAR-10 阶梯性不平衡数据集上的实验结果

图 3.15比较了不使用任何不平衡学习算法、随机过采样和随机降采样的泛化能力。从图中可以看出，对于该任务中使用的CNN模型，随机过采样方法可以在测试集上取得最优的分类准确率，并且不会导致更严重的过拟合。

4、不平衡学习的成果

上一节给出了不平衡学习算法的分类、几个经典算法的介绍和性能比较。本节将关注不平衡学习的研究进展，着重介绍两篇论文：

1)Lin, H.等人2018年发表在ACL上的《Adaptive Scaling for Sparse Detection in Information Extraction》

2)Huang, C.等人2016年发表在CVPR上的《Learning Deep Representation for Imbalanced Classification》

4.1 《Adaptive Scaling for Sparse Detection in Information Extraction》

4.1.1 引言

检测任务是信息抽取领域非常常见的任务，典型的任务如命名实体识别、关系抽取和事件检测等。在做检测任务时，我们可以把待检测的标签作为正例，其他标签作为反例，从而将检测任务转换为标准的分类任务。在这种分类任务中，一般使用交叉熵作为损失函数，正例的F值作为评价指标。由于正例(待检测的标签)往往非常稀疏，因此这是一个数据不平衡的分类任务。

 

 

可以看到，在计算F值时，正例和反例并非是等价的，这导致评估指标和优化目标出现了背离。因此在设计模型训练方法时，需要考虑到这种差异，尽量保证训练目标与评估指标的一致性。

一种做法是使用cost-sensitive的方法，对不同类别样本设置不同的损失权重，但在权重的设置上，过去的研究一般是手动设置或者是在大规模数据集上多次实验搜索得到，这些方法费时费力而且可迁移性较差。论文针对这一问题，提出一种自适应调整权重的算法，称为Adaptive Scaling。

4.1.2 Adaptive Scaling

Adaptive Scaling算法借鉴了经济学中的边际效用理论：指每新增(或减少)一个单位的商品或服务，它对商品或服务的收益增加(或减少)的效用。在分类任务中，将边际效用理论中的“商品或服务”替换为分类样本，收益即为评估指标(F值)，此时的边际效用定义为：每新增(或减少)一个分类正确(错误)的样本，它对评估指标F值增加(或减少)的效用。由此，可以使用每个类别对F值的边际效用作为其重要程度的衡量。

实际计算时，可以将评估指标对TP和TN的偏导值作为正例和反例的边际效用值。如果是把Accuracy作为目标，计算正例和反例的边际效用可以得到：

可以看到，当把Accuracy作为目标时，正例和反例的边际效用始终是恒定而且相等的，如果是将F值作为目标，可以得到：

 

 

这样就得到了能够自动在训练过程中调整样本权重的Adaptive Scaling算法，而且该算法不需要引入任何额外的超参数。相比于传统的cost-sensitive方法，其特点在于：

1)正例和反例的相对重要程度既与正反例的比例有关，也会受到当前模型的分类能力影响

2)反例的重要性会随着正例分类准确率的提升而增加

3)反例的重要性也会随着反例分类准确率的提升而增加

4)当precision比recall更重要时，反例的重要性也会增加

4.1.3 Batch-wise Adaptive Scaling

在训练神经网络时，最常用的是batch-wise的方法，如果用TP和TN在当前batch下的预测值作为近似，我们就得到了Batch-wise Adaptive Scaling算法。

具体来说，当前batch下，TP和TN的近似值按照下式计算：

 

 

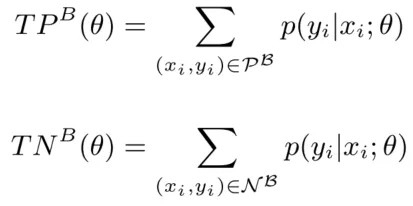
再忽略掉PE对结果的影响(比较微弱)，得到：

 

 

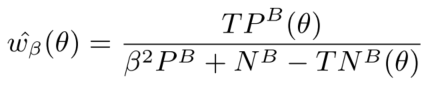
由此，在每个batch训练时，首先可以根据前向预测结果估计得到正例和反例的相对权重，然后计算cost-sensitive的交叉熵损失，最后反向传播更新模型参数。

可以将Batch-wise Adaptive Scaling视为一个插件，运行在前向预测和反向传播之间，不会影响到前后流程的正常运行。

4.1.4 实验验证

 

 

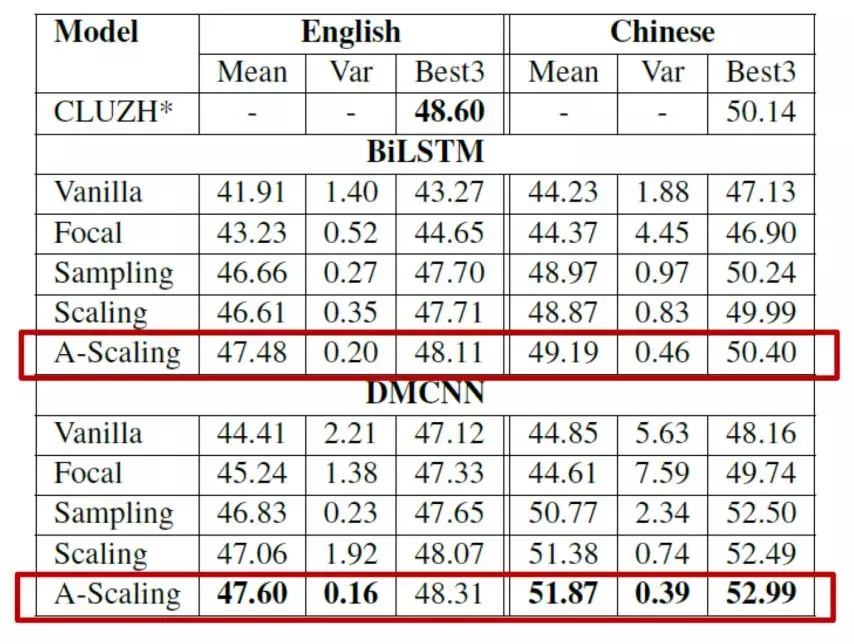
图 4.1 实验效果验证

论文在事件检测任务上进行了验证实验。测试数据为TAC KBP 2017 Event Nugget Detection Evaluation(LDC2017E55)官方提供的验证集，包含167篇英文文档和167篇中文文档。

图 4.1给出了多种算法的效果比较，可以看到，Adaptive Scaling(A-Scaling)算法几乎在各项指标上都达到了State-of-the-Art的效果。

 

 

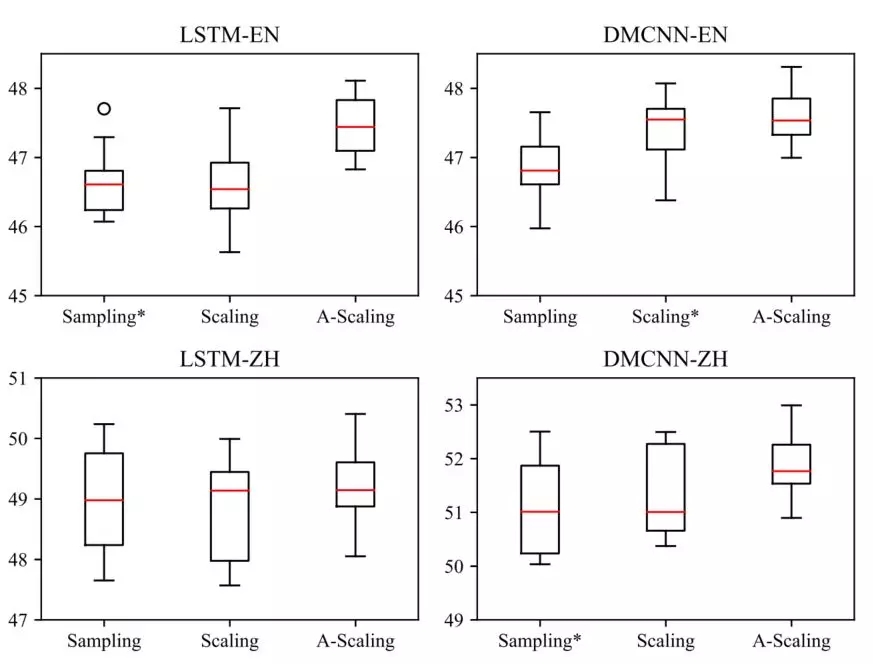
图 4.2 稳定性分析

图 4.2给出了多次实验下，不同算法结果的稳定性比较，同样可以看到，Adaptive Scaling算法在稳定性上也要好于传统的采样方法或者代价敏感型方法，尤其是在数据不平衡程度更高的中文数据集上，Adaptive Scaling表现明显更加稳定。

4.2 《Learning Deep Representation for Imbalanced Classification》

4.2.1 引言

计算机视觉领域的很多数据集都存在数据不平衡的问题。例如在人脸识别任务中，正例和反例的数据就极为不平衡。传统的应对数据不平衡的算法有采样方法和代价敏感型方法等，这些方法在经典的“浅层”机器学习算法上已经有充分的研究，但在深度学习模型上还缺乏系统的研究。

针对计算机视觉领域的数据不平衡问题，论文提出一种在不平衡数据下的更有效的深度表征并结合kNN做分类的算法：Large Margin Local Embedding (LMLE)-kNN(LMLE-KNN)。该算法包括2个步骤：首先使用CNN模型从不平衡数据集中学习得到每个样本的深度表征(embedding向量)，然后使用改进的k近邻分类算法对embedding向量分类。

4.2.2 从不平衡数据中学习深度表征

给定一个数据不均衡的计算机视觉数据集，论文希望先对每个样本学习一个embedding向量表示f(x)，学习到的embedding既具有区分性又能不包含本地的类别不均衡。为了实现这一目标，论文首先从不平衡数据中采样获取多个五元组，如图 4.3所示。

 

 

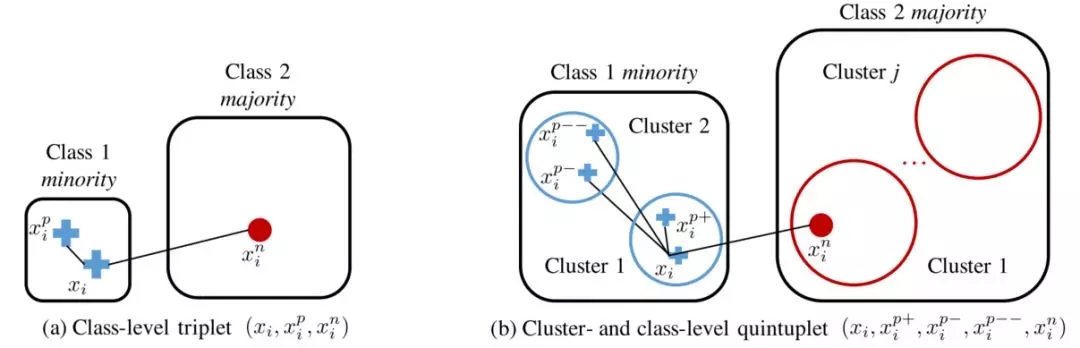
图 4.3 (a)传统的三元组表示 (b)五元组表示

 

 

相比于传统的三元组方法，这种五元组方法的优势在于：

1)五元组包括四个距离，这四个距离的大小需要满足一定的排序关系，这种排序关系可以提供更加丰富的信息和更强的约束。

2)尽管在做五元组采样时，我们会限制锚样本的采样概率分布使得来自少数类和多数类的数量尽量均衡，这种做法与降采样有些类似。但与降采样不同的是，由于这个采样过程会重复很多次，所以实际上并不会有降采样的信息丢失。

为了满足五元组四个距离的不等式要求，论文设计了一种三头的Hinge loss，表示如下：

 

 

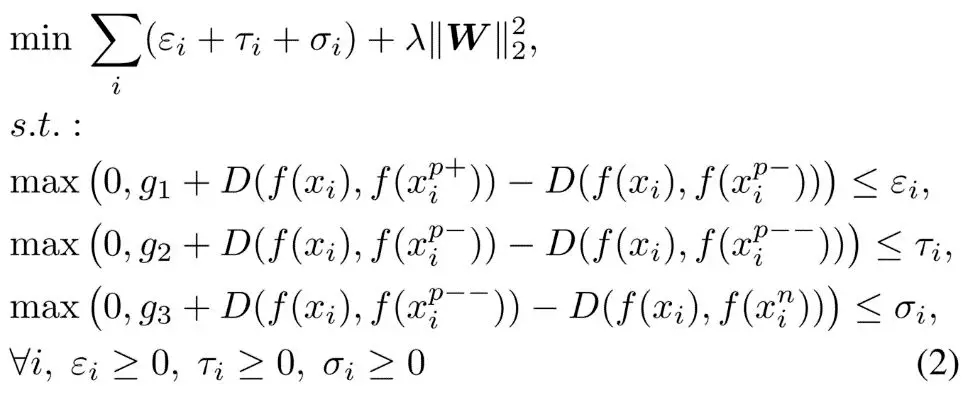
这个损失函数应用了Large Margin的思想，引入3个松弛变量限制了五元组四个距离的3个间隔。

论文使用CNN来生成对每张图片的深度表征，图 4.4示意了该CNN的的训练方法。

 

 

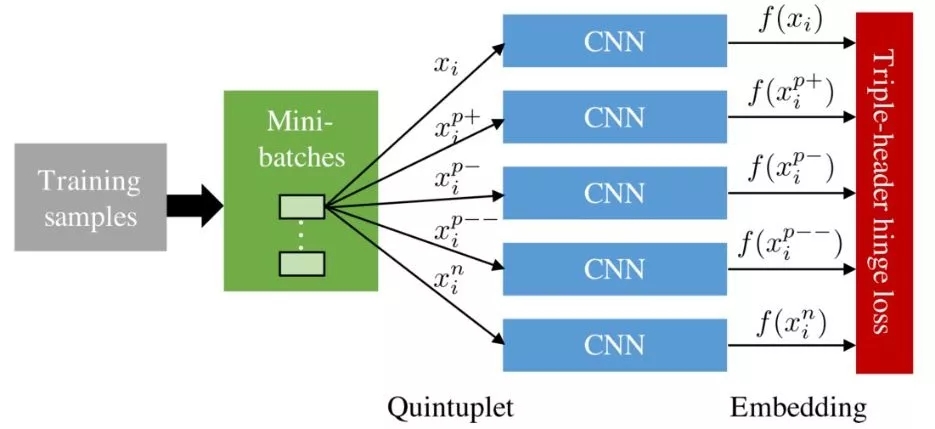
图 4.4 CNN模型训练

训练时，五元组的五个样本分别由同一个CNN做编码，获得5个embedding向量，然后计算三头的Hinge loss，最后经过反向传播更新CNN参数。

 

 

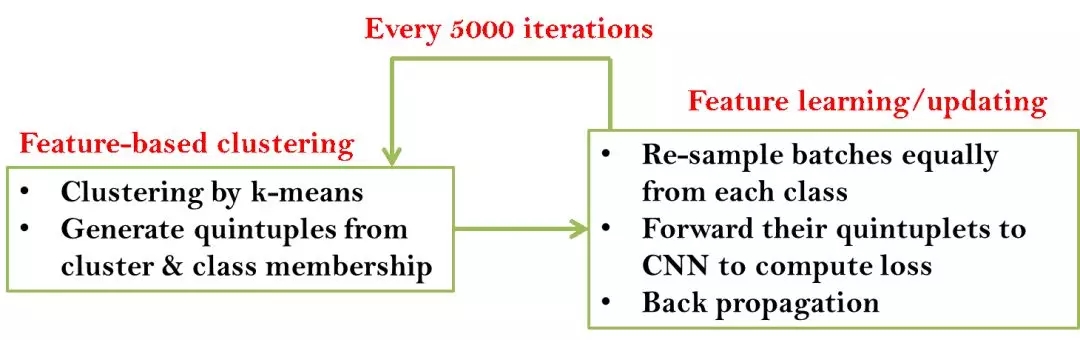
图 4.5 整体训练流程

图 4.5给出了训练获得样本数据深度表征的整体流程。

4.2.3 kNN不平衡数据分类

使用上一小节训练的CNN，可以获得对于数据集中每个样本的深度表征，在此基础上，论文设计了一种基于聚类cluster的kNN分类算法，用于做最终的分类。由于这一部分的算法与本文“不平衡学习”的主题没有关联，这里不再赘述，有兴趣的读者可以参阅Huang, C.等人的公开论文。

4.2.4 实验结果

论文在CelebA面部特性识别和BSD500边缘检测两个数据集上进行了实验，并与State-of-the-Art的方法做了比较。

 

 

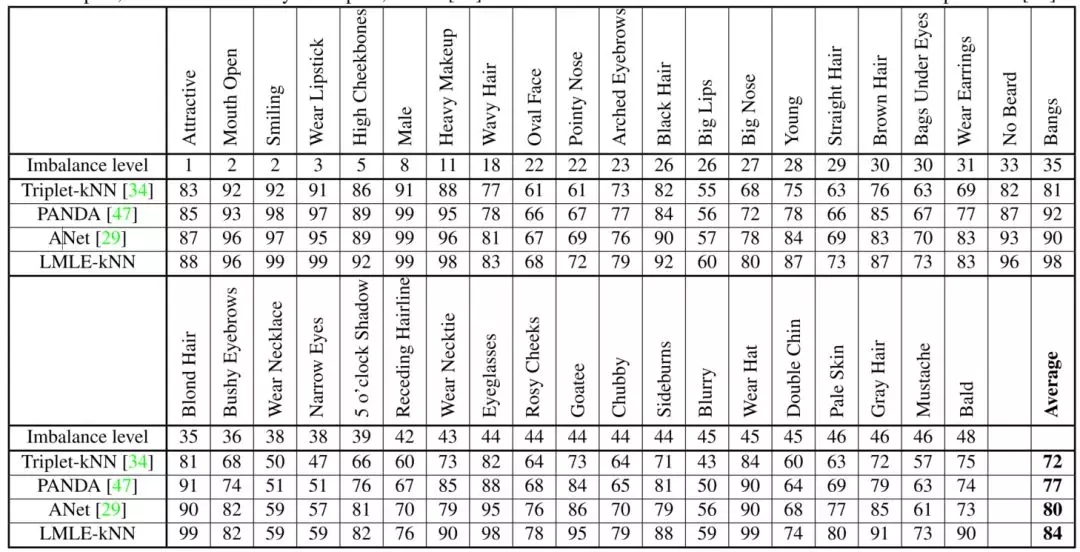
图 4.6 CelebA上的实验结果。Imbalance level的值越大，该特性数据的不平衡程度越高;评估指标为balanced accuracy=(TP/P + TN/N)/2。

 

 

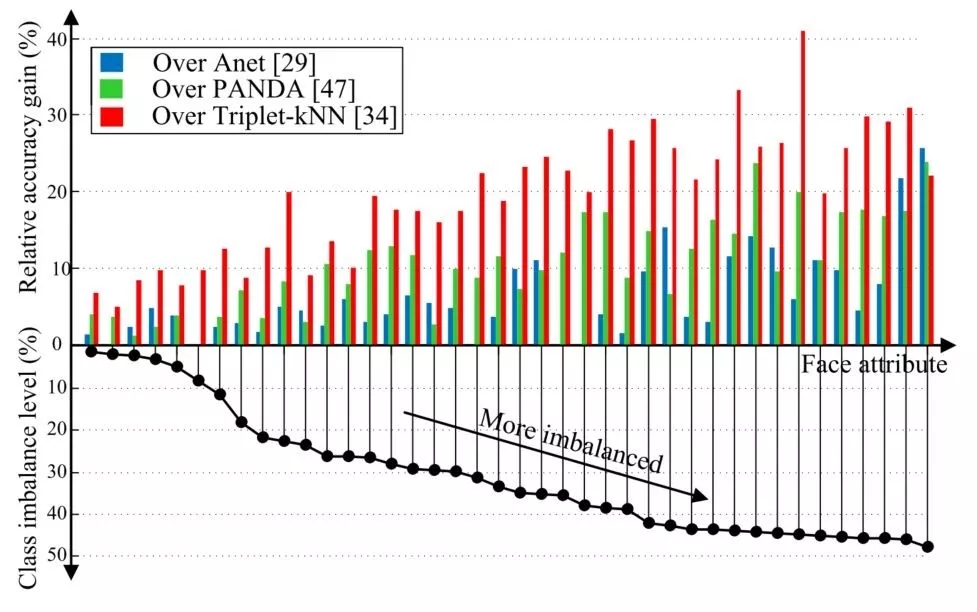
图 4.7 随数据不平衡程度增加的相对性能提升变化

图 4.6和图 4.7分别给出了在CelebA数据集上的实验效果比较和随数据不平衡程度增加的相对性能提升变化。可以看到，LMLE-kNN的分类效果明显优于其他State-of-the-Art方法，并且数据不平衡程度越高，LMLE-kNN在效果上的提升更加明显。

 

 

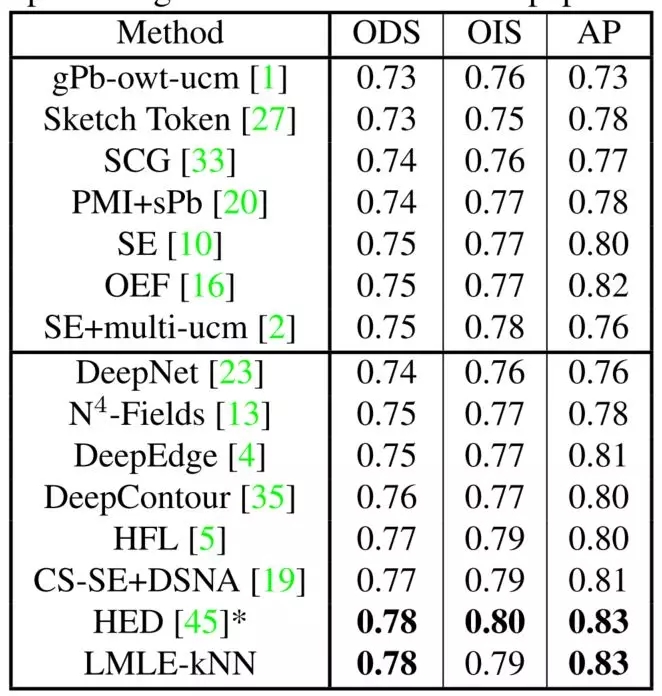
图 4.8 BSD500上的实验结果

图 4.8给出了在BSD500上的实验结果，LMLE-kNN算法同样取得了与State-of-the-Art方法相当的效果。需要说明的是，图中的HFL、HED等方法都使用了大型的VGGNet模型，而LMLE-kNN只使用了一个小型的6层CNN。

 

 

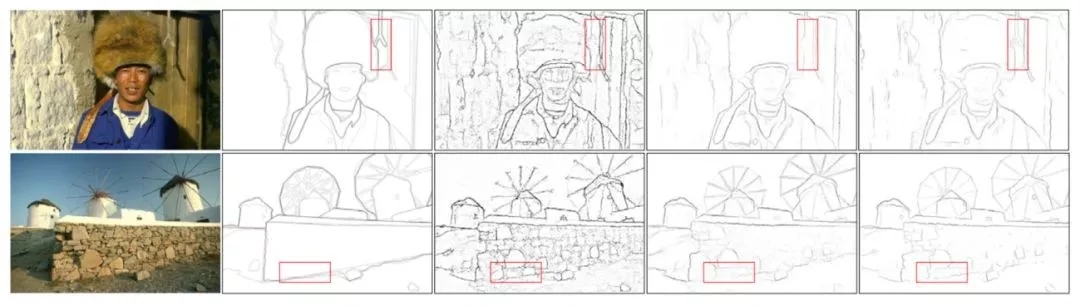
图 4.9 一个边缘检测的例子。从左到右依次为原始图像、理想结果、Sketch Token、DeepContour和LMLE-kNN的检测结果

图 4.9给出了一个具体的边缘检测例子，相比于其他算法，LMLE-kNN算法不会受到太多噪声边缘的影响。

5、总结

本文从不平衡学习的基础概念和问题定义出发，介绍了几类常见的不平衡学习算法和部分研究成果。总体来说，不平衡学习是一个很广阔的研究领域，但受笔者能力和篇幅的限制，本文仅对其中部分内容做了简单概述，有兴趣深入学习或研究的读者可以参阅下文所列参考文献或其他相关资料。

参考文献

[1]He, H., & Garcia, E. A. (2009). Learning from imbalanced data. IEEE Transactions on Knowledge & Data Engineering, 21(9), 1263-1284.

[2]Weiss, G. M. (2013). Foundations of Imbalanced Learning. Imbalanced Learning: Foundations, Algorithms, and Applications. John Wiley & Sons, Inc.

[3]He, H., & Ma, Y. (2013). Imbalanced Datasets: From Sampling to Classifiers. Imbalanced Learning: Foundations, Algorithms, and Applications. John Wiley & Sons, Inc.

[4]Galar, M., Fernandez, A., Barrenechea, E., Bustince, H., & Herrera, F. (2012). A review on ensembles for the class imbalance problem: bagging-, boosting-, and hybrid-based approaches. IEEE Transactions on Systems Man & Cybernetics Part C, 42(4), 463-484.

[5]Guo, H., Li, Y., Shang, J., Gu, M., Huang, Y., & Gong, B. (2016). Learning from class-imbalanced data: review of methods and applications. Expert Systems with Applications, 73, 220-239.

[6]Krawczyk, B. (2016). Learning from imbalanced data: open challenges and future directions. Progress in Artificial Intelligence, 5(4), 1-12.

[7]Lemaître, G., Nogueira, F., & Aridas, C. K. (2017). Imbalanced-learn: A python toolbox to tackle the curse of imbalanced datasets in machine learning. The Journal of Machine Learning Research, 18(1), 559-563.

[8]Zhou, Z., Shin, J., Zhang, L., Gurudu, S., Gotway, M., and Liang, J. (2017). Fine-tuning Convolutional Neural Networks for Biomedical Image Analysis： Actively and Incrementally. IEEE Conference on Computer Vision and Pattern Recognition . IEEE Computer Society.

[9]Li, S., Ju, S., Zhou, G., & Li, X. (2012). Active learning for imbalanced sentiment classification. Joint Conference on Empirical Methods in Natural Language Processing and Computational Natural Language Learning (Vol.27, pp.139-148). Association for Computational Linguistics.

[10]Buda, M., Maki, A., & Mazurowski, M. A. (2017). A systematic study of the class imbalance problem in convolutional neural networks.

[11]Huang, C., Li, Y., Chen, C. L., & Tang, X. (2016). Learning Deep Representation for Imbalanced Classification. IEEE Conference on Computer Vision and Pattern Recognition (pp.5375-5384). IEEE Computer Society.

[12]Lin, H., Lu, Y., Han, X., & Sun, L. (2018). Adaptive scaling for sparse detection in information extraction.
 

来自: 哈工大讯飞联合实验室

时间:2019-06-05 23:46  来源:    转发量:次