FTRL 公式推导

 

作者： 苏克 1900

写在前面：

本文主要参考Online Learning 算法理论与实践，但该文和网上找到的资料都没有很好的给出关于模型参数 w 的解析解的推导过程，甚至原论文http://www.eecs.tufts.edu/~dsculley/papers/ad-click-prediction.pdf还有一些符号错误。所以特此写个博文记录一下自己的推导过程。

一. 什么是 FTRL

首先介绍一下 FTL，FTL 的思想是每次找到让之前所有样本的损失函数之和最小的参数。流程如下：

初始化 w

for t = 1…n

损失函数 

更新

FTRL 算法就是在 FTL 的优化目标的基础上，加入了正则化，防止过拟合：

其中 R(w) 是正则项。

二. 代理损失函数

FTRL 的损失函数一般也不容易求解，这种情况下，一般需要找一个代理的损失函数。

代理损失函数需要满足以下条件：

1. 代理损失函数比较容易求解，最好是有解析解。
2. 代理损失函数求得的解，和原函数的解的差距越小越好

为了衡量条件 2 中的两个解的差距，引入 regret 的概念。

假设每一步用的代理函数是 

每次取：

而  是原函数的最优解，则：

 表示代理函数求出来的解离真正损失函数求出来的解的损失差距。

这个损失需要满足一定的条件，Online learning 才可以有效，即：

即随着训练样本的增加，代理损失函数和原损失函数求出来的参数的实际损失值差距越来越小。

三. 代理损失函数怎么选

如果  是凸函数，我们可以用下面的代理损失函数:

其中  是  的次梯度（如果  是可导的，次梯度就是梯度）。  满足：

为了产生稀疏的解，我们可以加入 L1 正则项：

只要  是凸函数，上面的代理函数一定满足：

四. 怎么得出 w 的解析解

取只和 w 相关的部分：

1. 当求得的 w 是大于等于 0 的时候：

其中  ，另上述偏导数等于 0，可得：

所以：

因为我们现在是讨论 w>=0 的解，而  大于 0（  大于 0），所以当：

 时，才符合我们的要求

而  大于 0。
令：

当  >=0 时，  是肯定大于 0 的，即不符合我们的要求。
：

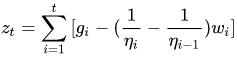当  <0 时，要满足  ，即 ，即  ，

所以有：

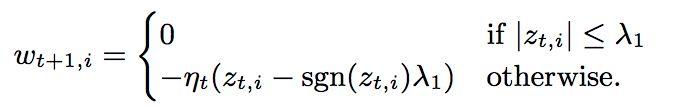
因为此时 

2. 当求得的 w 是小于 0 的时候：

令偏导数等于 0，可得：

因为我们现在是讨论 w<0 的解，而  大于 0（  大于 0），所以当：

 时，才符合我们的要求

而  大于 0。

令  ：

当  <=0 时，  是肯定小于 0 的，即不符合我们的要求。

当  >0 时，要满足  ，即 ，即  ，

所以有：

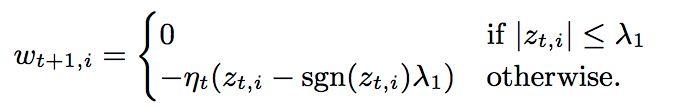
因为此时 

五. 为什么选择这个代理损失函数

参考在线学习算法 FTRL-Proximal 原理 - 雪伦的专栏 - CSDN 博客

重点是为什么说第一项是对损失函数的一个估计呢：

本人暂时说一个牵强的解释 (g 是 f 的梯度)：

根据泰勒展开公式：  ，如果  ，则：

就有了上述截图中类似的表达式子。

六. 遗留问题

1. 如果  不是凸函数，我们怎么选代理损失函数？
2. 什么是次梯度
3. 为什么只要  是凸函数，上面的代理函数一定满足：

未完待续。。。。

参考链接：

Online Learning 算法理论与实践

在线学习算法 FTRL-Proximal 原理 - 雪伦的专栏 - CSDN 博客

时间:2019-05-10 23:02  来源:    转发量:次