贝叶斯网络基础（Probabilistic Graphical Models）

from http://www.cnblogs.com/nobkb/p/3510495.html

本篇博客是Daphne Koller课程Probabilistic Graphical Models(PGM)的学习笔记。

概率图模型是一类用图形模式表达基于概率相关关系的模型的总称。概率图模型共分为三个部分，分别为表示理论，推理理论和学习理论。基本的概率图模型包括贝叶斯网络、马尔科夫网络和隐马尔科夫网络。

---

Student Example

一个学生，拥有成绩、课程难度、智力、SAT的分、推荐信等变量。

通过一张图可以把这些变量的关系表示出来，可以想象成绩由课程难度和智力决定，SAT成绩由智力决定，而推荐信由成绩决定。

在这个例子中，将变量简单化，建立一个CPD（Conditional probability distribution）条件概率密度。按下表进行假设：

变量	值	含义
d	0、1	课程简单、课程难
i	0、1	智力一般、智力超常
g	A、B、C	课程获得A、B、C的成绩
s	0、1	SAT成绩一般、成绩优秀
l	0、1	无推荐信、有推荐信

 

 

 

 

 

并表示为下图：

 

 

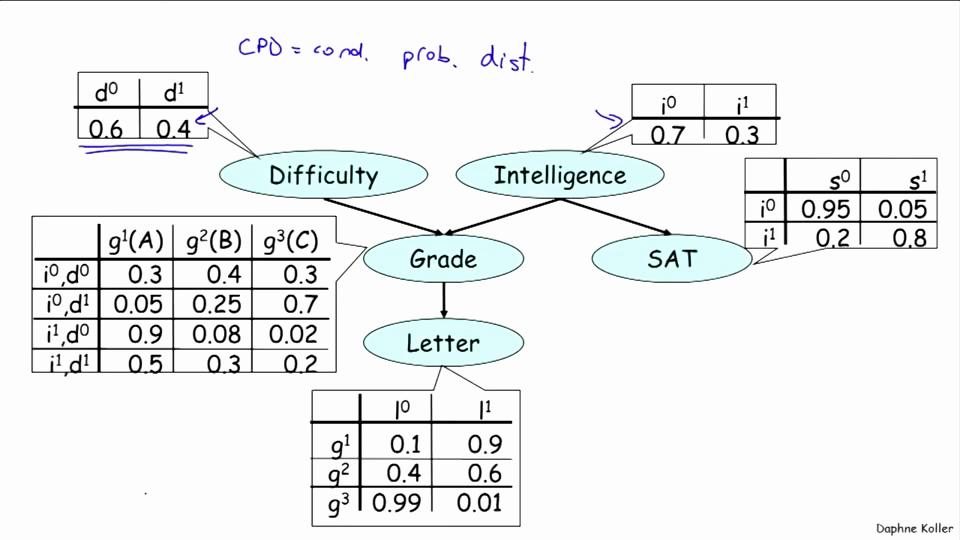
使用概率中的chain rule，可以将上图的整体概率表示为：

 

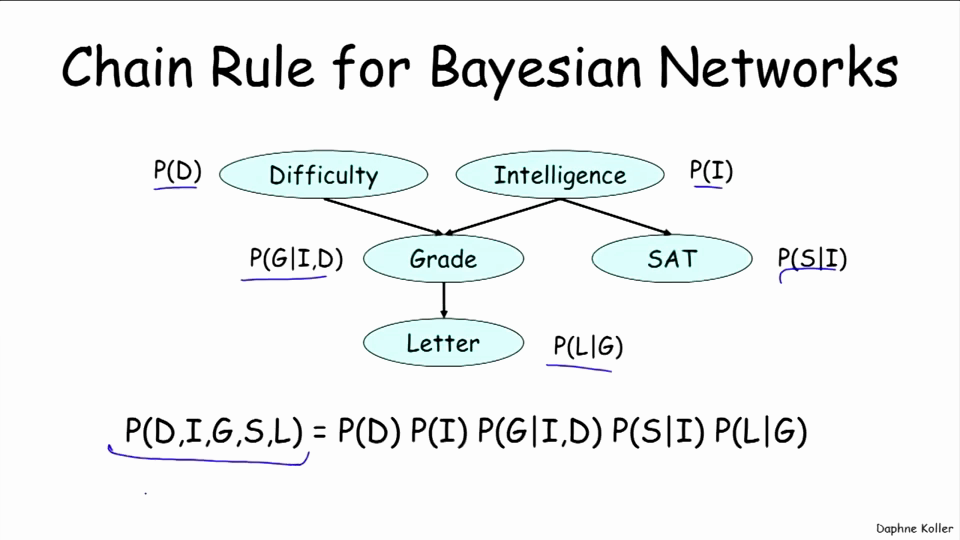
比如说P(d₀, i₁, g₃, s₁, l₁)的概率就等于0.6*0.3*0.02*0.8*0.01。

贝叶斯网络定义为：

1. 一个有向无环图表示随机变量x₁…x_n。
2. 每个节点都有一个CPD，是一个父节点的条件概率分布。
3. BN可以表示为一个联合概率分布。

其中有一些性质：

1. 每个BN的P>=0
2. 所有BN的P和为1

令G为一个关于x1…x_n的贝叶斯网络，如果G的联合概率密度能够表达为链式P，则称P factorizes over G。

 

Genetic Inheritance Example

以一个家族的血型作为研究对象。每个节点是每一个家庭成员的血型（即显血型），隐节点则为遗传血型。显血型包括A、B、O、AB，而遗传血型则包括AA、AB、AO、AO、BB、OO。

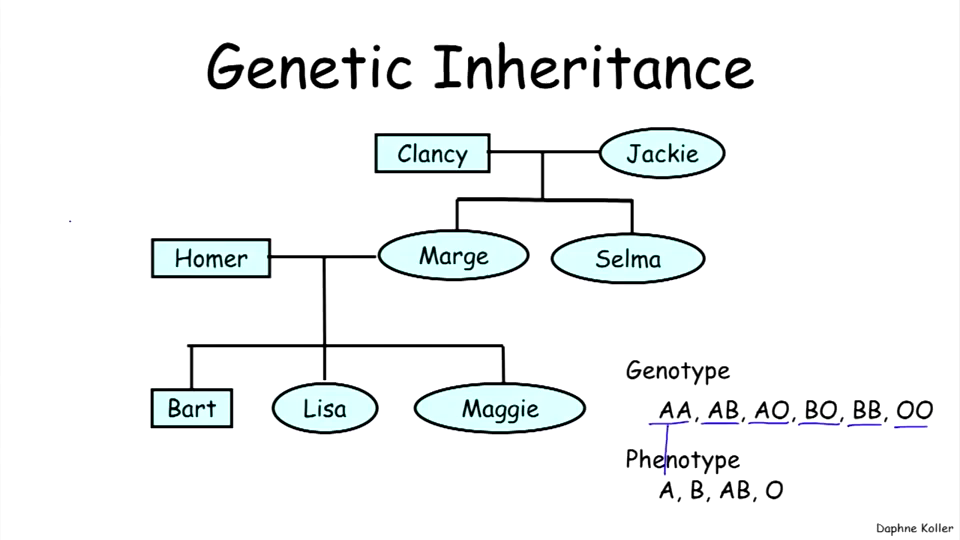
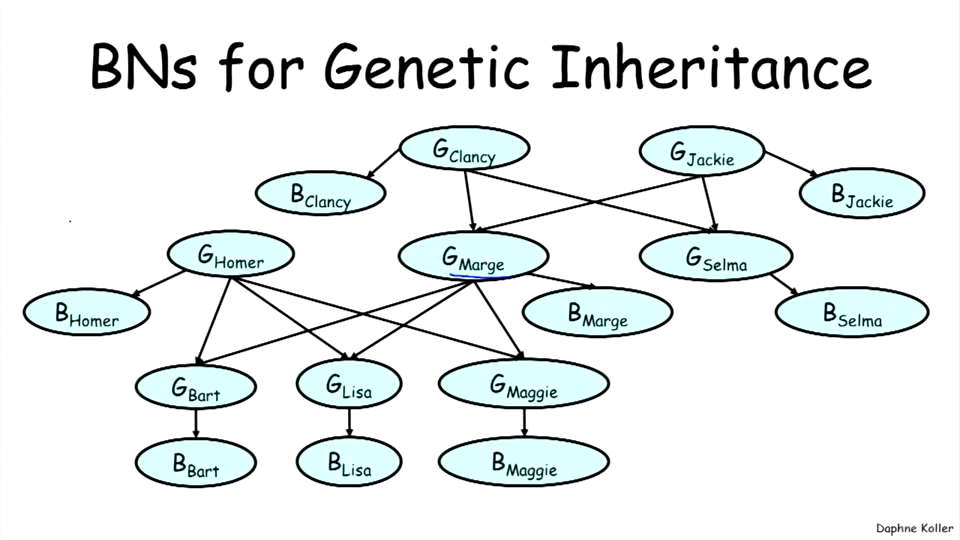
模式推理：

•  因果推理

因果推理从顶向下，以父节点或者祖先节点为条件。

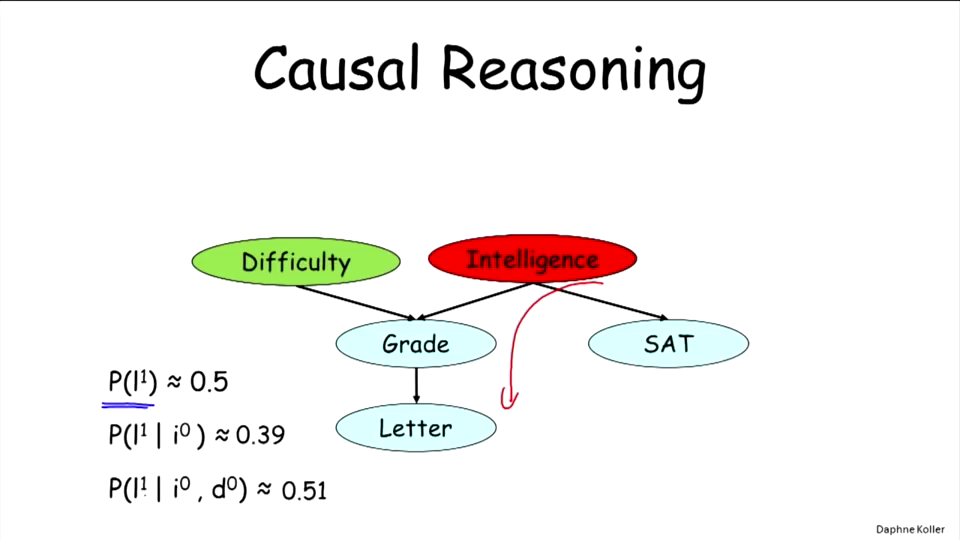
• 证据推理

证据推理从下向上，以子孙节点为条件。

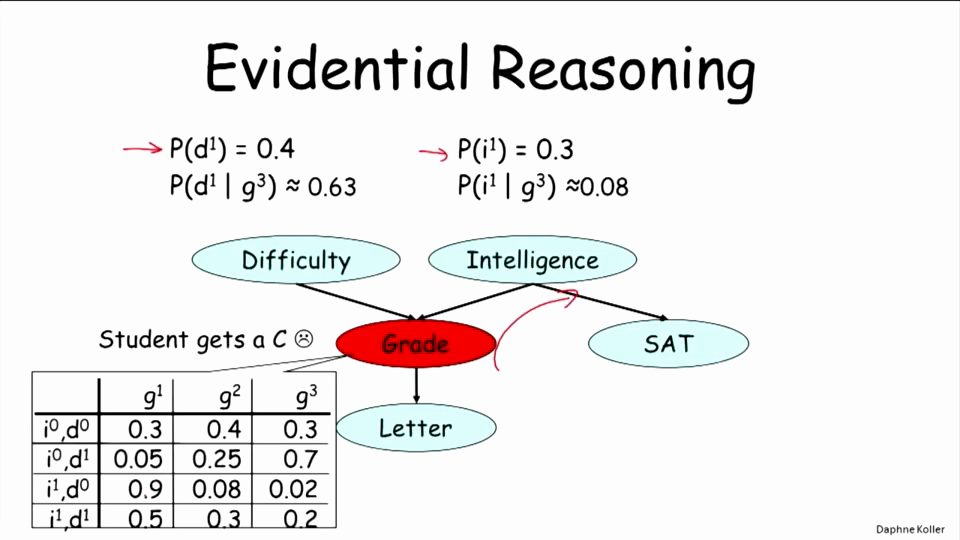
• Intercausal Reasoning(原因之间的推理？？)

方向是横向的，以其他原因和结果为条件。

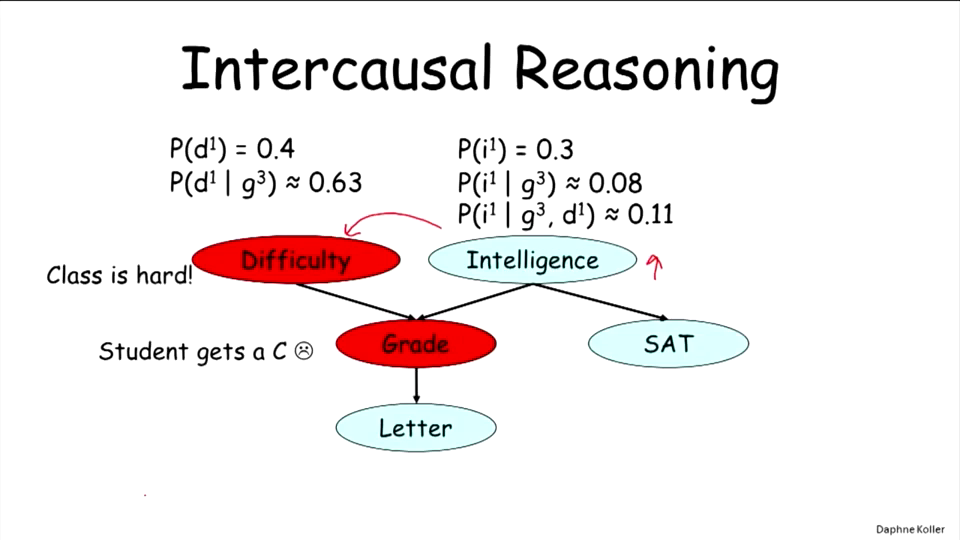
在贝叶斯网络中，满足一定条件，变量之间就会概率相关，这个之后会提到，比如下例：某学生Grade为C，SAT成绩优异，那么该门课程太难的概率为多少呢。

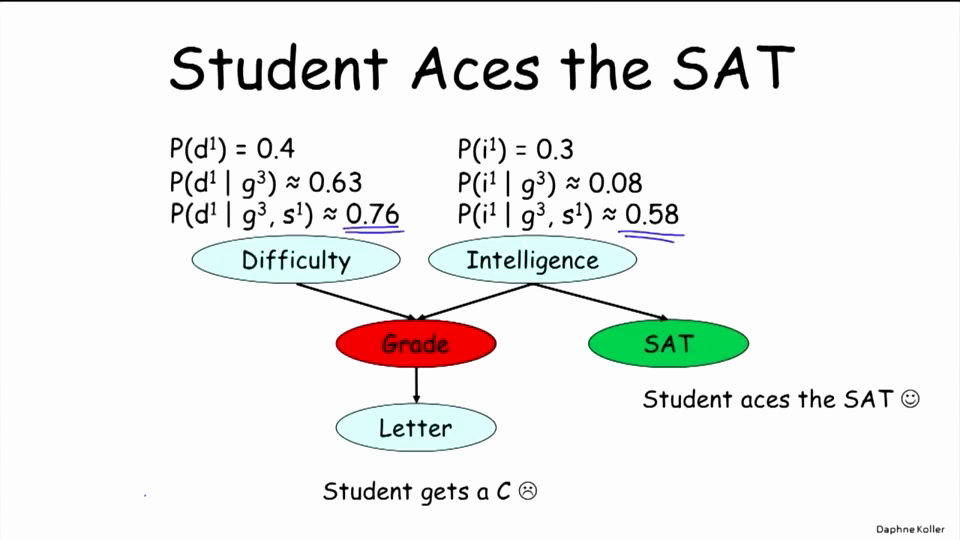
概率影响流：

X–>Y　　　　　D会影响G

X<–Y　　　　　G会影响G

X–>W–>Y　　D会影响到L

X<–W<–Y　　知道L，影响对L的估计

X<–W–>Y　　知道G，也会影响对S的估计

X–>W<–Y　　知道D，不会影响对I的估计，这种被称为V结构。

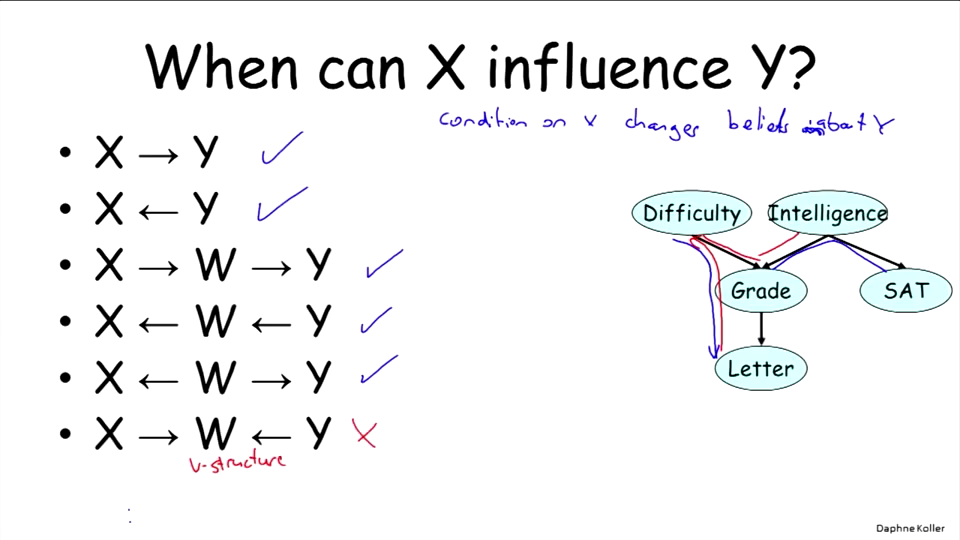
除了V结构，概率影响的流动是顺畅的。

在给出条件Z的情况下，X与Y还是相互影响的吗？

X–>Y　　　　有弧直接相连，相互影响

X<–Y　　　　有弧直接相连，相互影响

下面的四种要分两种情况考虑，1：W不是Z的子集，2：W是Z的子集

X–>W–>Y　　以DGL为例　　1：条件S下，D会影响L　　　　2：条件G下，D不影响L

X<–W<–Y　　以LDG为例　　1：条件S下，L会影响D　　　   2：条件G下，L不影响D

X<–W–>Y　　以GIS为例　　1：条件D下，S会影响G　　　　2：条件I下，G不影响S

X–>W<–Y　　以DGI为例　　1：条件S下，D不影响I　　　　 2：条件G下，D影响I

对于X–>W<–Y，可以扩展为W的子孙。比如，在条件L下，D也会影响到I。

对于轨迹x₁—x_n，激活这条路径的条件为：

1. 对于任何V结构，x_i-1–>x_i<–x_i+1，x_i或者它的子孙节点必须为观察值。
2. 对于其他的x_i，必须不为观察值。

贝叶斯网络中的独立：

当在条件Z的情况下，X和Y在G中没有一条激活的路径（acvitve trail），则称X和Y在图G中是d-separated。

如果P factorizes over G，则在条件Z下d-separated的X和Y满足条件Z下的独立性。

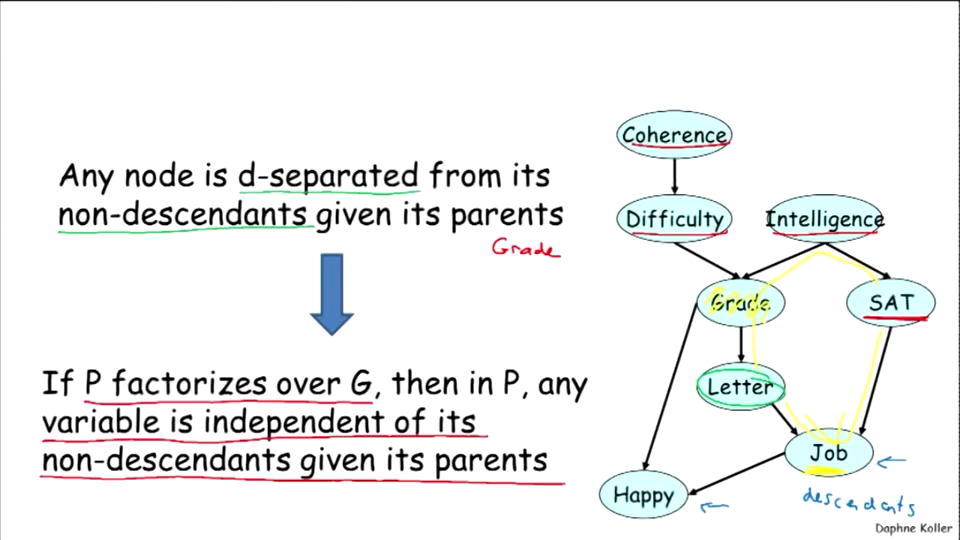
在BN中，出给X，则以X的父节点为条件，X与任何它的非子孙d-separated。

下图中，Letter与SAT、Intelligence、Difficulty、Coherence都d-separated，也就以为着L与S、I、D、C都概率独立。

Imaps:

G中所有的d-separation，都对应P满足的一个相互独立。所以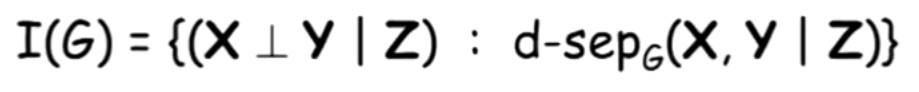当P满足I(G)时，G为P的一个Imap，当G为空集时，是所有P的I-map。

有下列理论：

• 如果P factorizes over G，那么G是P的一个I-map。
• 如果G是P的一个I-map，那么P factorizes over G。

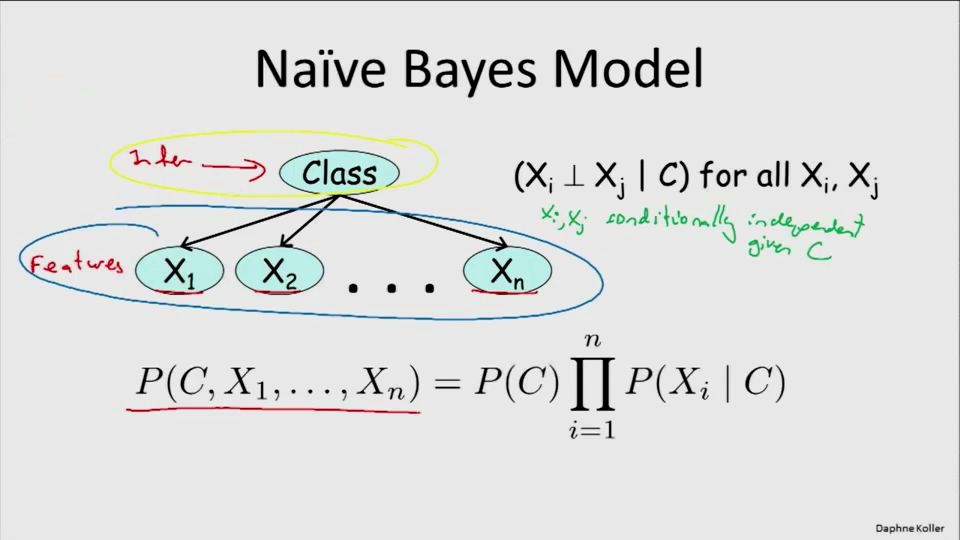
朴素贝叶斯：

贝叶斯模型：一个样本具有n个特征，而每个特征关于类别的条件概率分布是相互独立的。

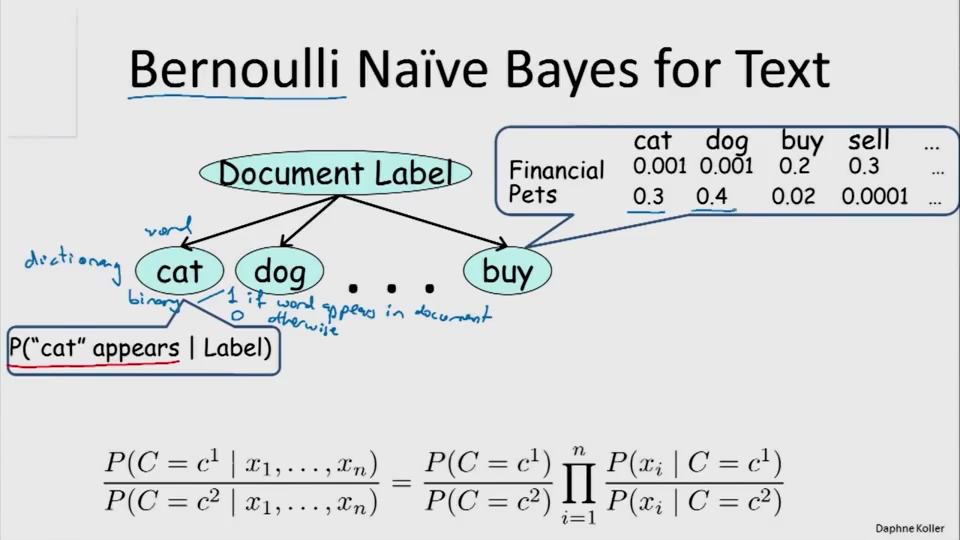
文本的伯努利朴素贝叶斯分类：

对于许多文本，分别关于宠物、财经或者其他。有N个特征作为字典，字典中包括“cat”、“dog”、“buy”，而每个特征都是一个伯努利分布。

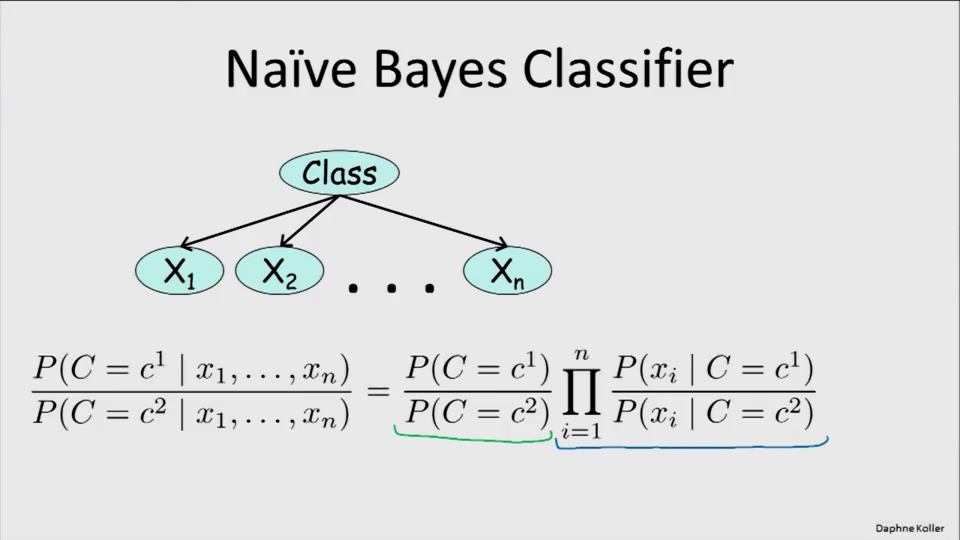
根据贝叶斯公式，在x₁…x_n条件下，可以求出C=C1与C=C2的比。

介绍两种朴素贝叶斯的分类：

1. 伯努利朴素贝叶斯分类
2. 多项式朴素贝叶斯分类

第一种：以字典为特征，特征数量为字典中单次总数。每一个特征都是伯努利分布的，整个树可以表述成一个CPD。它的假设是：在Label条件下，每一个字出现的概率与其他字出现的概率是不相关的，这是有违常识的。所以伯努利朴素贝叶斯分类仅仅是一个not bad的方法。

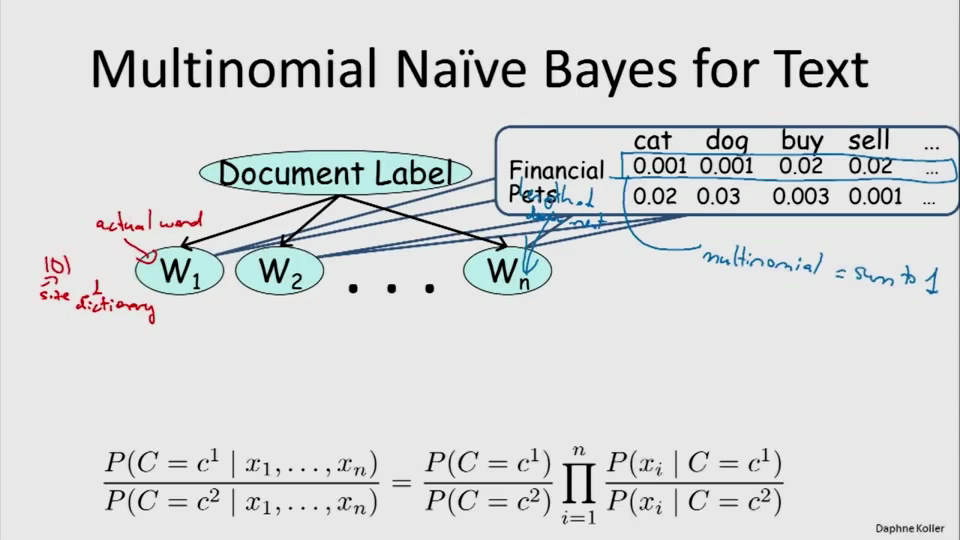
第二种：以每个单词为特征，特征数量为文档的长度，每一个特征都是一个多项式分布，每个特征的CPD可以不同也可以相同。它的假设是：在Label条件下，一个字在位置a出现的概率与这个字才位置b出现的概率是不相关的。这种分类被广泛使用。

 

总结：

朴素贝叶斯分类是一种简单的分类方法，拥有计算效率和容易构建的优点，在处理弱相关特征时有惊人的效率，但是由于强独立性的假设，当特征是相关的时候，使用朴素贝叶斯分类效果不好。

时间:2019-04-19 23:34  来源:    转发量:次