测试机器学习降维之线性判别模型 (LDA)

 

拍摄于无锡古镇

1.LDA 简介

线性判别分析 (Linear Discriminant Analysis, LDA) 是一种监督学习的降维方法，也就是说数据集的每个样本是有类别输出。和之前介绍的机器学习降维之主成分分析 (PCA)方法不同，PCA 是不考虑样本类别输出的无监督学习方法。LDA 的原理简单来说就是将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点会形成按类别区分。而我们的目标就是使得投影后的数据，类间方差最大，类内方差最小。

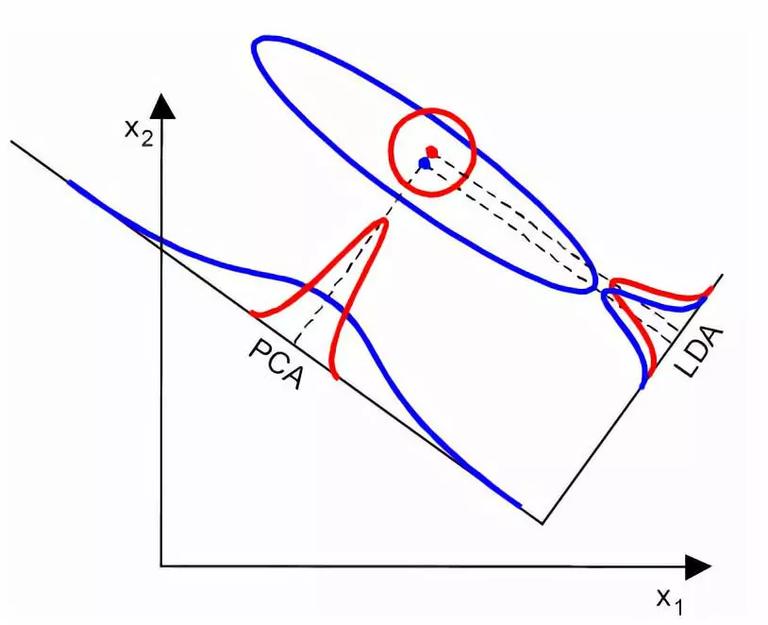
以下图为例，假设有两类数据，分别为红色和蓝色。现在我们希望，将这些数据投影到一维的直线上，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

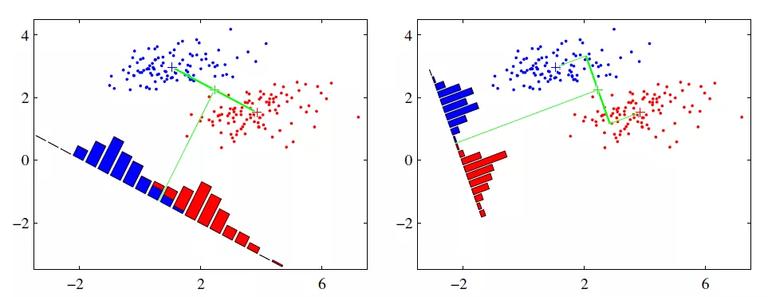
从上图的两种投影方式能够看出，右图能够更好的满足我们的目标，即类间方差最大，类内方差最小。下面我们来看看 LDA 内部原理，如何达到我们所希望的目标。

2. 瑞利商和广义瑞利商

介绍 LDA 原理之前，我们先了解一些数学知识，即瑞利商 (Rayleigh quotient)与广义瑞利商 (genralized Rayleigh quotient)。首先来看看瑞利商的函数 R(A,x)

瑞利商 R(A,x) 有一个非常重要的性质，即它的最大值等于矩阵 A 的最大特征值，而最小值等于矩阵 A 的最小特征值，即满足

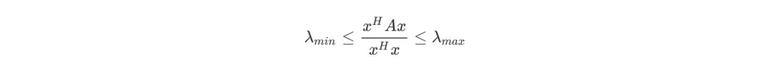
以上就是瑞利商的内容，现在看看广义瑞利商内容，广义瑞利商函数 R(A,B,x)

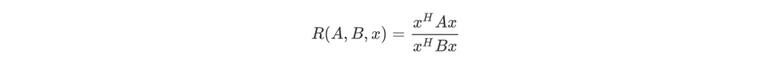
其中 x 为非零向量，而 A,B 为 n*n 的 Hermitan 矩阵，B 是正定矩阵。那么 R(A,B,x) 的最大值和最小值是什么呢？

3. 二类 LDA 原理

4. 多类 LDA 原理

5.LDA 算法流程

6.LDA vs PCA

LDA 和 PCA 有很多相同点和不同点，我们来对比看看两者的区别。

相同点

• 两者均可对数据进行降维。

• 两者在降维时均使用了矩阵特征分解的思想。

• 两者都假设数据符合高斯分布。

不同点

• LDA 是有监督的降维方法，而 PCA 是无监督的降维方法。

• LDA 降维最多降到类别数 k-1 的维数，而 PCA 无此限制。

• LDA 选择分类性能最好的投影方向，而 PCA 选择样本点投影具有最大方差的方向。

不同数据情况下，LDA 和 PCA 降维方法各有优劣。例如某些数据情况下 LDA 比 PCA 方法更好

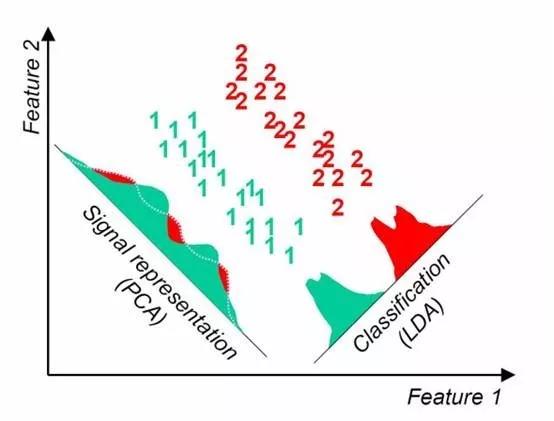
某些数据情况下 PCA 比 LDA 方法降维更好

7.LDA 算法总结

LDA 优点

• 在降维过程中可以使用类别的先验知识经验，而 PCA 这种无监督学习则无法使用类别先验知识。 

LDA 缺点

• LDA 可能过度拟合数据。

• LDA 不适合对非高斯分布样本进行降维，PCA 也有这个问题。

• LDA 降维最多降到类别数 k-1 的维数，如果我们降维的维数大于 k-1，则不能使用 LDA。

你看到的这篇文章来自于公众号「谓之小一」，欢迎关注我阅读更多文章。

时间:2019-02-20 18:18  来源:    转发量:次