机器学习经典图

图片收集自网络，仅供学习和交流。

1. 为什么低训练误差并不总是一件好的事情呢？

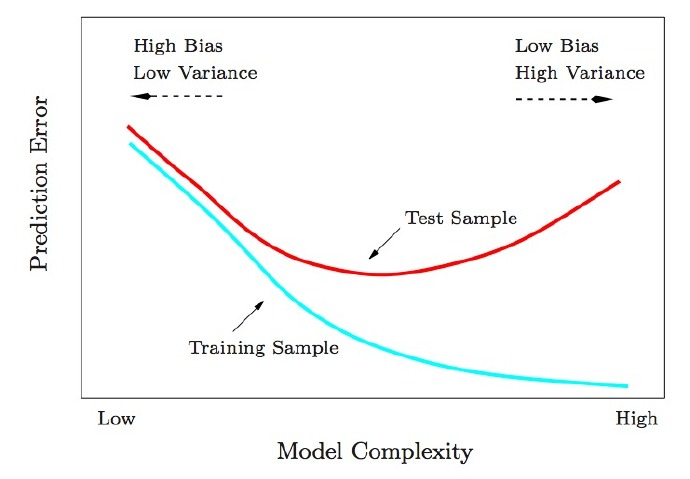
答：因为模型的复杂性

2. 低度拟合或者过度拟合的例子

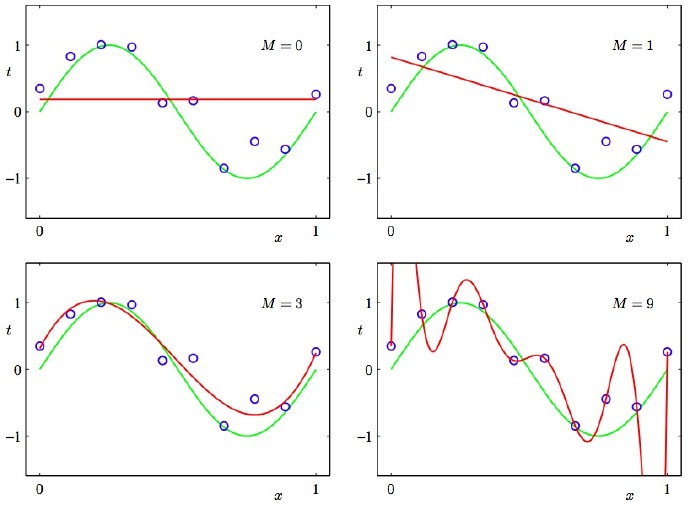
3. 为什么贝叶斯推理可以具体化奥卡姆剃刀原理

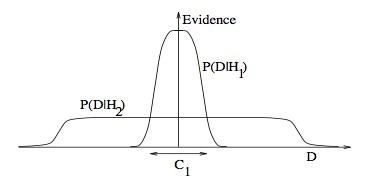
答：首先知道奥卡姆剃刀原理：切勿浪费较多东西去做，用较少的东西，同样可以做好的事情。上图已经非常直接：较少的前提条件或许能得到更广泛的结果。

4. 为什么集体相关的特征单独来看时无关紧要？

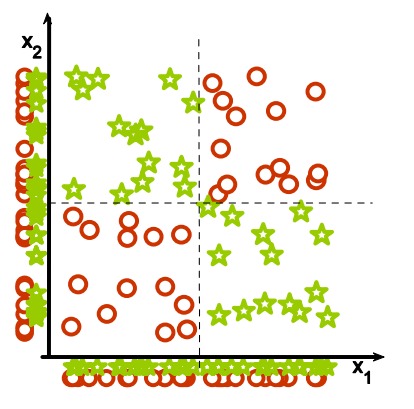
答：如上图，数据是二维的，映射到单个维度来看就是泛泛的、无意义的。

5. 为什么无关紧要的特征会损害KNN？

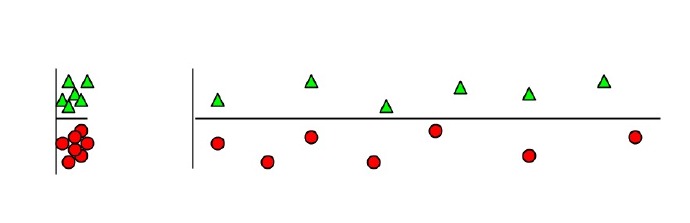
答：如上图，横轴为无关紧要特征，因为横轴特征的出现，将原本鲜明的聚类特征模糊化，纵轴权重被横轴稀释，从而得到错误的聚类结果。

6. 非线性的基础函数是如何使一个低维度的非线性边界的分类问题，转变为一个高维度的线性边界问题的？

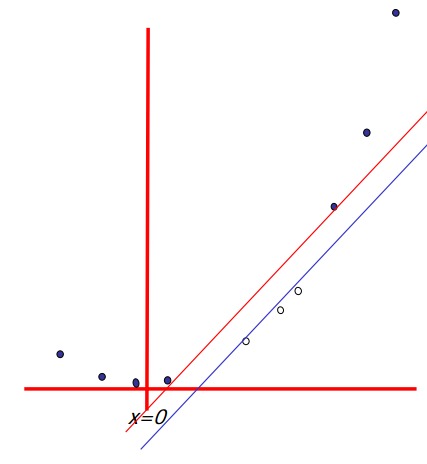
答：此条与第4点相对应，与第5点相反。即低维线性不可分的数据，投射到高维也许线性可分。核函数也是这个原理。

7. 为什么判别式学习比产生式更加简单？

答：首先知道，判别式模型（Discriminative Model）是直接对条件概率p(y|x;θ)建模。常见的判别式模型有 线性回归模型、线性判别分析、支持向量机SVM、神经网络等。

生成式模型（Generative Model）则会对x和y的联合分布p(x,y)建模，然后通过贝叶斯公式来求得p(yi|x)，然后选取使得p(yi|x)最大的yi。

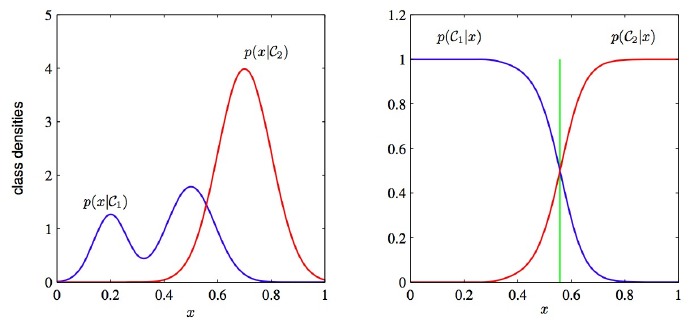
已知特征x的情况下，左图为生成式：需要根据已知训练集的分类，统计该分类下特征出现概率，求出全概率，然后求出某个特征属于某一分类的概率，概率最大的分类即为最终分类。左图描绘了求解联合概率的第一步，图形复杂。

右图为判别式：直接对条件概率p(Ci|x)建模，即某一特征属于某一分类的概率，图形简单明了。

8. 学习算法可以被视作优化不同的损失函数？

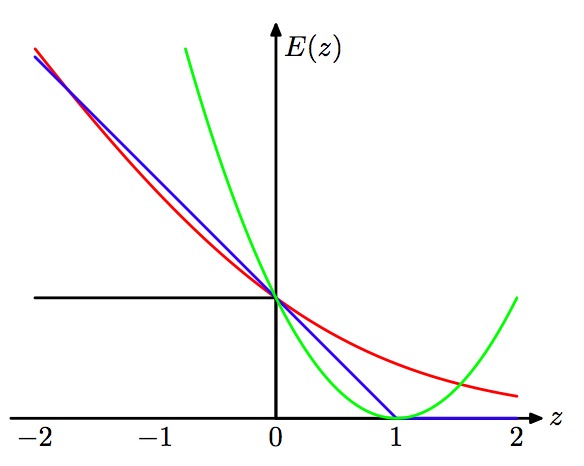
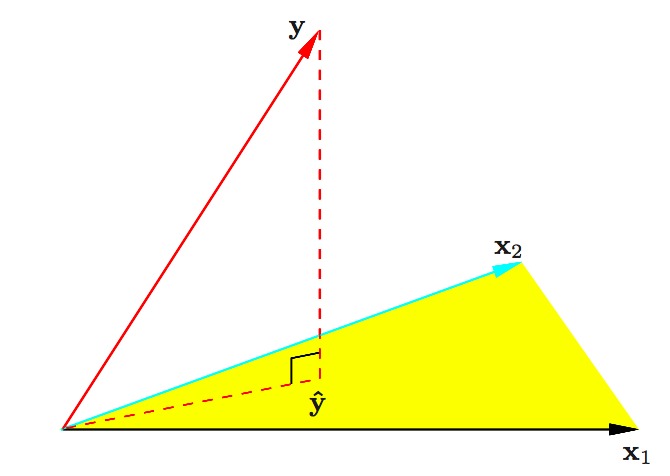
9. 带有两个预测的最小二乘回归的N维几何图形。

10. 链式求导。

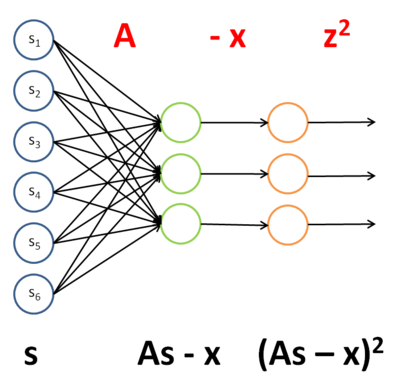
11. 特征工程大图

时间:2019-01-19 00:14  来源:    转发量:次