蚂蚁金服核心技术：百亿特征实时推荐算法揭秘

阿里妹导读：本文来自蚂蚁金服人工智能部认知计算组的基础算法团队，文章提出一整套创新算法与架构，通过对 TensorFlow 底层的弹性改造，解决了在线学习的弹性特征伸缩和稳定性问题，并以 GroupLasso 和特征在线频次过滤等自研算法优化了模型稀疏性，在支付宝核心推荐业务获得了 uvctr 的显著提升，并较大地提升了链路效率。

0. 综述

在线学习 (Online learning) 由于能捕捉用户的动态行为，实现模型快速自适应，进而成为提升推荐系统性能的重要工具。然而它对链路和模型的稳定性，训练系统的性能都提出了很高的要求。但在基于原生 TensorFlow，设计 Online 推荐算法时，我们发现三个核心问题：

• 一些资讯推荐场景，需要大量长尾词汇作为特征，需使用 featuremap 对低频特征频次截断并连续性编码，但耗时且方法 aggressive。

• 使用流式数据后，无法预知特征规模，而是随训练逐渐增长。因此需预留特征空间训练几天后重启，否则会越界。

• 模型稀疏性不佳，体积达到数十 GB，导致上传和线上加载耗时长且不稳定。

更重要的是，在线学习如火如荼，当流式特征和数据都被打通后，能按需增删特征，实现参数弹性伸缩的新一代训练平台成为大势所趋。为了解决这些问题，从 2017 年底至今，蚂蚁金服人工智能部的同学，充分考虑蚂蚁的业务场景和链路，对 TensorFlow 进行了弹性改造， 解决了以上三大痛点，简化并加速离线和在线学习任务。其核心能力如下：

• 弹性特征伸缩体系，支持百亿参数训练。

• group_lasso 优化器和频次过滤，提高模型稀疏性，明显提升线上效果。

• 模型体积压缩 90%，完善的特征管理和模型稳定性监控。

在与业务线团队的共同努力下，目前已在支付宝首页的多个推荐场景全流量上线。其中某推荐位的个性化 online learning 桶最近一周相比线上多模型融合最优桶提升 4.23% ， 相比随机对照提升达 34.67% 。 某个性化资讯推荐业务最近一周，相比 DNN 基准 uv-ctr 提升 +0.77%，pv-ctr 提升 +4.78%，模型体积压缩 90%，链路效率提升 50%。

1. 弹性改造及优势

背景：在原生 TensorFlow 中，我们通过 Variable 来声明变量，若变量超过了单机承载的能力，可使用 partitioned_variables 来将参数分配到不同机器上。 但必须指定 shape，声明后即不可改变，通过数组索引查找。

由于推荐系统中大量使用稀疏特征，实践中一般采取 embedding_lookup_sparse 一类的方法在一个巨大的 Dense Variable 中查找向量并求和，来代替矩阵乘法。开源 Tensorflow 限定了 Variable 使用前必须声明维度大小，这带来了两个问题：

1）需要预先计算特征到维度范围内的 int 值的映射表，这一步操作通常在 ODPS 上完成。因为需要扫描所有出现的特征并编号，计算非常缓慢；

2）在 online learning 场景下，为了容纳新出现的特征，需要预留一部分维度空间，并在线上不断修改映射表，超过预留空间则需要重新启动在线任务。

为了突破固定维度限制，实现特征的动态增加和删除，最朴素的优化想法是在 TensorFlow 底层实现模拟字典行为的 Variable，并在此基础上重新实现 Tensorflow 上层 API。由此我们进行了优化，在 server 新增了基于 HashMap 的 HashVariable，其内存结构如下：

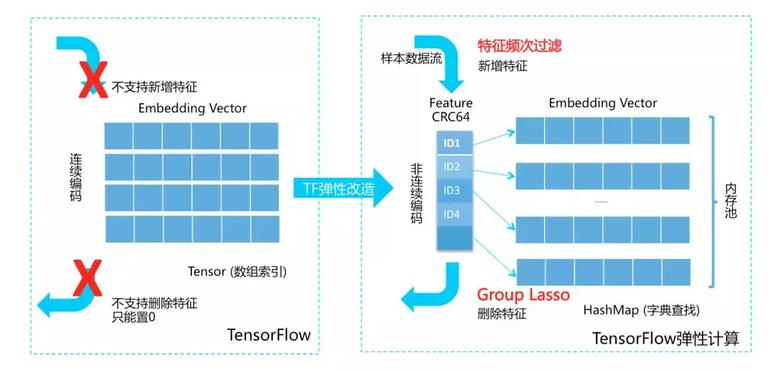
在声明该变量时，只需增加一句，其他训练代码皆不需改动：

每个特征都通过 hash 函数映射到一个 2 的 64 次方大小的空间内。当需要计算该特征时，PS 会按需惰性创建并返回之。但其上层行为与原生 TF 一致。由于去掉了 featuremap 转 ID 的过程，我们内部形象地将其称为“去 ID 化”。在此之上我们实现了 Group Lasso FTRL，频次过滤和模型压缩等一系列算法。

备注：弹性特征带来一个显著的优势：只要用足够强的 L1 稀疏性约束，在单机上就能调试任意大规模的特征训练，带来很多方便。我们的 hashmap 实现是 KV 化的，key 是特征，value 是 vector 的首地址。

离线训练优化

经过这样的改造后，在离线批量学习上，带来了以下变化：

 

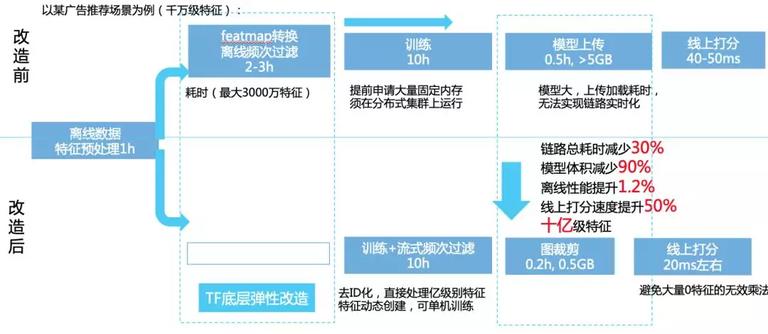
在线训练优化

online learning 上，能带来如下变化：

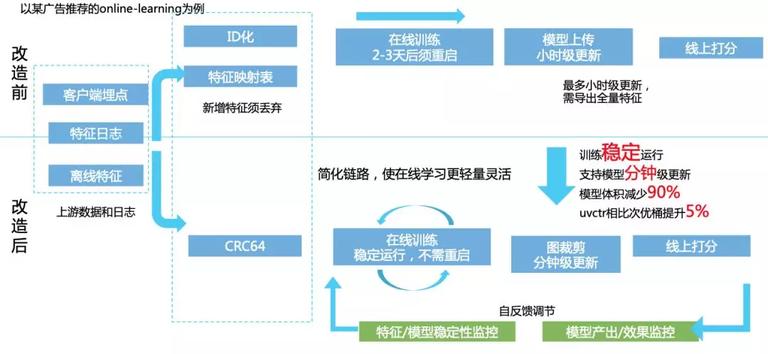
除了性能有明显的提升之外，其最大的优势是不需提前申请空间，训练可以无缝稳定运行。

2. 特征动态增删技术

弹性架构，主要目的就是特征优选，让模型自适应地选择最优特征，进而实现稀疏化，降低过拟合。本节介绍特征优选的两个核心技术：

• 使用流式频次过滤， 对特征进入进行判定。

• 使用 Group Lasso 优化器，对特征进行筛选和删除。

 

2.1 Group  Lasso 优化器

稀疏化是算法追求的重要模型特性，从简单的 L1 正则化和 Truncated Gradient[9]， 再到讨论累积梯度平均值的 RDA(Regularized Dual Averaging)[10]， 再到目前常见的 FTRL[2] 。 然而它们都是针对广义线性模型优化问题提出的稀疏性优化算法，没有针对 sparse DNN 中的特征 embedding 层做特殊处理。把 embedding 参数向量当做普通参数进行稀疏化，并不能达到在线性模型中能达到的特征选择效果，进而无法有效地进行模型压缩。

例如：当包含新特征的样本进入时，一个特征对应的一组参数（如 embedding size 为 7，则参数数量为 7）被激活，FTRL 判定特征中的部分参数无效时，也不能安全地将该特征删除。如图：

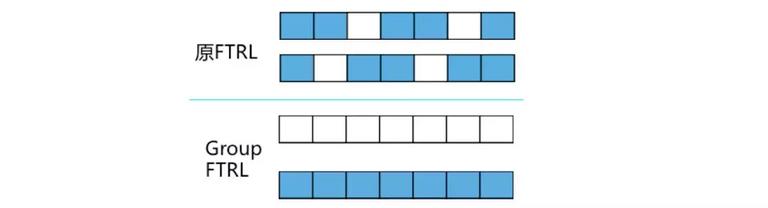
因此，在 L1 和 L2 正则的基础上，人们引入 L21 正则 (group lasso) 和 L2 正则(exclusive sparsity)，分别表示如下：

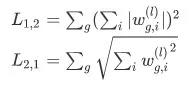
L21 早在 2011 年已经引入，它最初目的是解决一组高度关联特征（如男 \ 女）应同时被保留或删除的问题，我们创新地扩展到 embedding 的表示上，以解决类似的问题。

在 L21 中，由于内层 L2 正则将一个特征的所有参数施加相同的约束，能将整组参数清除或保留，由此决定 embedding 层中的某些特征对应的 embedding 向量是否完全删除，提升模型泛化性。因此称为 group lasso。

而 L12 则正好相反，它迫使每组参数中的非 0 参数数量一致但值又尽可能不同，但使输出神经元互相竞争输入神经元，进而使特征对目标更具区分性。

对于 DNN 分类网络，底层表示要求有足够的泛化性和特征抽象能力，上层接近 softmax 层，需要更好的区分性。因此我们通常在最底层的 embedding 层使用 group lasso。即如下的优化目标：

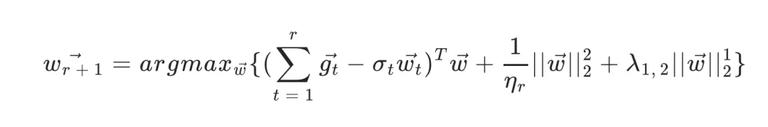
直接将 L21 正则项惩罚加入 loss，模型最终也能收敛，但并不能保证稀疏性。因此 Group lasso 优化器参考了 FTRL，将梯度迭代分成两个半步，前半步按梯度下降，后半步微调实现稀疏性。通过调节 L1 正则项（即公式中的λ），能有效地控制模型稀疏性。

Group lasso 是弹性计算改造后，模型性能提升和压缩的关键。值得指出：

1. 在我们实现的优化器中，Variable，以及 accum 和 linear 两个 slot 也是 KV 存储。

2. L12 和 L21 正则相结合的方法也已经有论文讨论 [8]，但我们还未在业务上尝试出效果。

3. 由于篇幅限制，本节不打算详细介绍 Group lasso 的原理和推导

 

2.2 流式频次过滤

讨论完特征动态删除的方法后，我们再分析特征的准入策略。

2.2.1 频次过滤的必要性

在 Google 讨论 FTRL 的文章 1 中提到， 在高维数据中大部分特征都是非常稀疏的，在亿级别的样本中只出现几次。那么一个有趣的问题是，FTRL 或 Group FTRL 优化器能否能删除 (lasso) 极低频特征？

在 RDA 的优化公式中，满足以下条件的特征会被置 0：

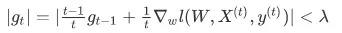
若在 t 步之前，该特征只出现过几次，未出现的 step 的梯度为 0，随着步数增大，满足上述条件变得越来越容易。由此 RDA 是可以直观处理极稀疏特征的。 但对于 FTRL，要满足：

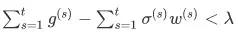
其中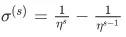， 不仅和历史梯度有关，还与历史学习率和权重 w 有关。 因此 FTRL 虽然也能处理极稀疏特征，但并没有 RDA 那么 aggressive（此处还待详细地分析其下界，Group FTRL 与此类似）。

由于 FTRL 在设计和推导时并未明确考虑极低频特征，虽然通过增大λ，确实能去除大量极低频特征，但由于约束太强，导致部分有效特征也被 lasso，在离线实验中被证明严重影响性能。其次，对这些巨量极低频特征，保存历史信息的工程代价是很高昂的（增加几倍的参数空间和存储需求），如下图：

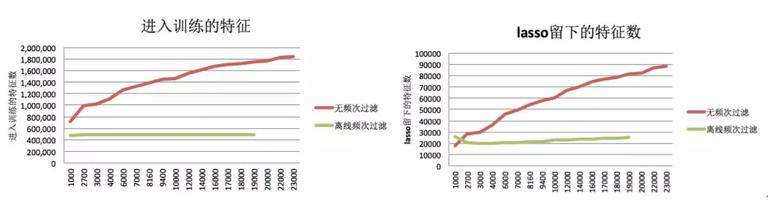
因此我们提出，能否在实时数据流上模拟离线频次过滤，为特征提供准入门槛，在不降低模型性能的基础上，尽量去除极低频特征，进一步实现稀疏化？

2.2.2 频次过滤的几种实现

注意： 由于默认的 embedding_lookup_sparse 对特征执行了 unique 操作（特征归一化以简化计算），因此在 PS 端是不可能获取真实特征和 label 频次的。需要 Python 端对 placeholder 统计后，上传给 server 端指定的 Variable，优化器通过 slot 获得该 Variable 后作出联合决策。

最 naive 的思路是模拟离线频次过滤，对特征进行计数，只有达到一定阈值后再进入训练，但这样破坏了数据完整性：如总频次 6，而阈值过滤为 5，则该特征出现的前 5 次都被忽略了。为此我们提出了两种优化方案：

• 基于泊松分布的特征频次估计

在离线 shuffle 后的特征满足均匀分布，但对在线数据流，特征进入训练系统可看做泊松过程，符合泊松分布：

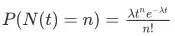
其中 n 为当前出现的次数，t 为当前的步数，λ为单位时间发生率，是泊松分布的主要参数，T 为训练总步数。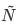为特征最低门限（即最少在 T 时间内出现的次数）。

因此我们能通过前 t 步的特征出现的次数 n，将 t 时刻当做单位时间，则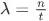。 根据泊松分布，我们可以算出剩余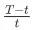时间内事件发生大于等于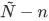次的概率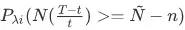。 每次该特征出现时，都可按该概率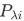做伯努利采样，特征在 t 步进入系统的概率用下式计算：

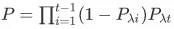
通过真实线上数据仿真，它能接近离线频次过滤的效果，其λ是随每次特征进入时动态计算的。它的缺陷是：

1. 当 t 越小时，事件发生在 t 内的次数的 variance 越大，所以会以一定概率误加或丢弃特征。

2. 未来总的训练步数 T 在在线学习中是未知的。

3. 频次过滤与优化器相分离，导致不能获得优化器的统计信息。

• 动态调 L1 正则方案

在经典的 FTRL 实现中，L1 正则对每个特征都是一致的。这导致了 2.2.1 中提到的问题：过大的 L1 虽然过滤了极低频特征，但也影响的了模型的性能。参考各类优化器（如 Adam）对 learning_rate 的改进，我们提出：通过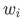特征频次影响 L1 正则系数，使得不同频次的特征有不同的 lasso 效果。

特征频次和基于 MLE 的参数估计的置信度相关，出现次数越低置信度越低。如果在纯频率统计基础上加入一个先验分布（正则项），当频率统计置信度越低的时候，越倾向于先验分布，相应的正则系数要更大。我们经过多个实验，给出了以下的经验公式：

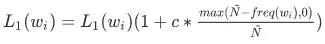
其中 c 是惩罚倍数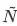，为特征最低门限，这两者皆为超参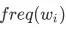，是当前特征出现的频次。

我们在线上环境，使用了动态调节 L1 正则的方案 。在 uvctr 不降甚至有些微提升的基础上，模型特征数比不使用频次过滤减少 75%，进而从实验证明了频次过滤对稀疏化的正向性。它的缺点也很明显：特征频次和正则系数之间的映射关系缺少严谨证明。

频次过滤作为特征管理的一部分，目前还少有相关论文研究，亟待我们继续探索。

3. 模型压缩和稳定性

3.1 模型压缩

在工程上，由于做了优化，如特征被优化器 lasso 后，只将其置 0，并不会真正删除；在足够多步数后才删除。同时引入内存池，避免特征的反复创建和删除带来的不必要的性能损失。 这就导致在训练结束后，模型依然存在大量 0 向量。导出时要进一步做模型压缩。

由于引入了 HashPull 和 HashPush 等非 TF 原生算子，需要将其裁剪后转换为原生 TF 的 op。 我们将这些步骤统称图裁剪 (GraphCut)， 它使得线上 inference 引擎，不需要做任何改动即可兼容弹性改造。由于有效特征大大减少，打分速度相比原引擎提升 50% 以上。

我们将图裁剪看做 TF-graph 的静态优化问题，分为 3 个步骤：

• 第一遍遍历 Graph，搜索可优化子结构和不兼容的 op。

• 第二遍遍历，记录节点上下游和元数据，裁剪关键 op，并将 Variable 的非 0 值转存至 Tensorflow 原生的 MutableDenseHashTable。本步骤将模型体积压缩 90%。

• 拼接新建节点，重建依赖关系，最后递归回溯上游节点，去除与 inference 无关的子图结构

我们实现了完整简洁的图裁剪工具，在模型热导出时调用， 将模型从原先的 8GB 左右压缩到几百兆大小，同时保证模型打分一致。

3.2 模型稳定性和监控

online learning 的稳定性非常重要。我们将线上真实效果，与实时模型生成的效果，进行了严密的监控，一旦样本偏差过多，就会触发报警。

由于需捕捉时变的数据变化，因而不能用固定的离线数据集评估模型结果。我们使用阿里流式日志系统 sls 最新流入的数据作为评估样本，以滑动窗口先打分后再训练，既维持了不间断的训练，不浪费数据，同时尽可能高频地得到最新模型效果。

我们对如下核心指标做了监控：

• 样本监控： 正负比例，线上打分值和 online-auc(即线上模型打分得到的 auc)，产出速率，消费速率。

• 训练级监控： AUC, User-AUC(参考备注)，loss, 模型打分均值（与样本的正负比例对齐），异常信息。

• 特征级管理： 总特征规模，有效 /0/ 删除特征规模，新增 / 插入 / 删除的速率。

• 整体模型和调度：模型导出的时间，大小，打分分布是否正常，是否正常调度。

• 业务指标：uvctr,pvctr(小时级更新，T+1 报表)。

线上与训练指标之间的对应关系如下表：

通过 http 接口，每隔一段时间发送监控数据，出现异常会及时产生钉钉和邮件报警。下图是对 9 月 20 日到 27 号的监控，从第二张图表来看，模型能较好的适应当前数据流的打分分布。

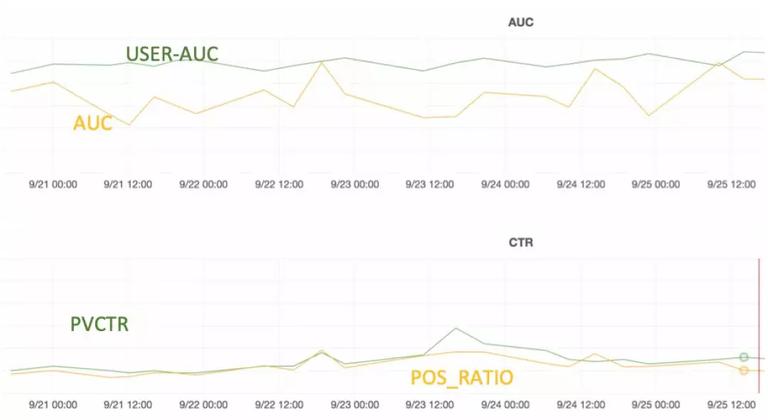
User-AUC：传统的 AUC 并不能完全描述 uvctr，因为模型很可能学到了不同用户间的偏序关系，而非单个用户在不同 offer 下的点击偏序关系。为此，我们使用了 User-AUC，它尽可能地模拟了线上 uvctr 的计算过程，在真实实验中，监控系统的 uvctr 小时报表，与实时模型输出的 User-AUC 高度一致。

4. 工程实现和效果

目前算法已经在支付宝首页的多个推荐位上线。推荐系统根据用户的历史点击，融合用户画像和兴趣，结合实时特征，预估用户 CTR，进而提升系统整体点击率。

我们以推荐位业务为例说明，其采用了经典的 wide&deep 的网络结构，其 sparse 部分包含百级别的 group(见下段备注 1)。 一天流入约百亿样本，label 的 join 窗口为固定时长。由于负样本占大多数，上游链路对正负样本做了 1：8 的降采样 (见下文备注 2)。

训练任务采用蚂蚁统一训练平台构建，并使用工作流进行定时调度，离线和在线任务的其他参数全部一致。Batchsize 为 512，每 200 步（即 20 万样本）评估结果，定时将模型通过图裁剪导出到线上系统。当任务失败时，调度系统会自动拉起，从 checkpoint 恢复。

该推荐业务的 online learning 桶最近一周相比线上多模型融合最优桶提升 4.23% ， 相比随机对照提升达 34.67% 。 另一资讯推荐业务其最近一周，相比 DNN 基准 uv-ctr 提升 +0.77%，pv-ctr 提升 +4.78%。实验效果相比有较大的提升。

备注 1： group embedding 是将相似 emb 特征分组，各自 lookup 求和后再 concat，使得特征交叉在更高层进行。其设计是考虑到不同 group 的特征差异很大 (如 user 和 item)，不应直接对位求和。

备注 2： inference 打分仅做 pointwise 排序，采样虽改变数据分布但不改变偏序关系，因此并未在训练上做补偿。

5. 未来工作

弹性特征已经成为蚂蚁实时强化深度学习的核心要素。它只是第一步，在解决特征空间按需创建问题后，它会带来一个充满想象力的底层架构，众多技术都能在此基础上深挖： 在工程上，可继续从分钟级向秒级优化，进一步提升链路实时性并实现模型增量更新； 在算法上，我们正在探索如样本重要性采样，自动特征学习，在线线性规划与 DNN 的结合，实现优化器联合决策等技术。

由于在线学习是个复杂的系统工程，我们在开发和调优时遇到了大量的困难，涉及样本回流，训练平台，模型打分，线上评估等一系列问题，尤其是稳定性，但基本都一一克服。为了保证线上结果稳定可信，我们在观察和优化两三个月后才发布这篇文章，希望和业界同仁一起交流探讨。

本文作者为蚂蚁金服人工智能部认知计算组的基础算法团队，团队涉及图像、NLP、推荐算法和知识图谱等领域，拥有定损宝和理赔宝等核心业务。

参考文献：

[1] McMahan, Brendan. “Follow-the-regularized-leader and mirror descent: Equivalence theorems and l1 regularization.” Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics. 2011.

[2] McMahan, H. Brendan, et al. “Ad click prediction: a view from the trenches.” Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2013.

[3]Yuan, Ming, and Yi Lin. “Model selection and estimation in regression with grouped variables.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 68.1 (2006): 49-67.

[4] Andrew, Galen, and Jianfeng Gao. “Scalable training of L 1-regularized log-linear models.” Proceedings of the 24th international conference on Machine learning. ACM, 2007.

[5]Scardapane, Simone, et al. “Group sparse regularization for deep neural networks.” Neurocomputing 241 (2017): 81-89.

[6] Yang, Haiqin, et al. “Online learning for group lasso.” Proceedings of the 27th International Conference on Machine Learning (ICML-10). 2010.

[7]Zhou, Yang, Rong Jin, and Steven Chu–Hong Hoi. “Exclusive lasso for multi-task feature selection.” Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics. 2010.

[8] Yoon, Jaehong, and Sung Ju Hwang. “Combined group and exclusive sparsity for deep neural networks.” International Conference on Machine Learning. 2017.

[9] Langford, L. Li, and T. Zhang. Sparse online learning via truncated gradient.JMLR, 10, 2009.

[10]L. Xiao. Dual averaging method for regularized stochastic learning and online optimization. In NIPS, 200

时间:2019-01-07 00:20  来源:    转发量:次