简单聊聊特征工程

随着大数据时代的到来，特征工程发挥着越来越重要的作用。那么什么是特征工程呢，简单说，就是发现对因变量 y 有明显影响作用的特征，通常称自变量 x 为特征，特征工程的目的是发现重要特征。

一般来说，特征工程大体上可以分为三个方面，一是特征构造 ，二是特征选择 ，，三是特征生成 。三个方面当中，最重要的是特征选择，我们先简单说一下，特征构造和特征生成，后面再说特征选择。当然一个特征工程当中并不一定涉及到这三个方面。那么接下来，先说特征构造。

顾名思义，特征构造就是构造出来新的特征，一般都是通过对原有的特征进行四则运算产生新的特征。比如原来的特征是 x1 和 x2，那么 x1+x2 就是一个新的特征，或者当 x1 大于某个数 c 的时候，就产生一个新的变量 x3，并且 x3=1，当 x1 小于 c 的时候，x3=0，所以这样看来呢，可以按照这种方法构造出很多特征，这个就是构造。

我们再来说说特征生成，特征生成和特征构造有些相似，但是还是存在一些区别的，特征生成的话，比如主成分分析或者因子分析，都可以对原有数据进行特征生成，比如卷积神经网络的卷积层就是一个特征生成的过程，一张图片，经过卷积的不断扫描，就会把原始图片里边的好多特征逐步提取出来，这个就是特征生成。再如通过主成分分析对原始数据进行降维，那么降维后，每个主成分其实就代表一个新的特征，同样因子分析也具有这方面的功能，通过因子分析可以把潜在变量后面的潜在因子找出来。

通过这几个例子，大家可以逐渐感觉到特征构造和特征生成会有一些区别，但是也有一定的联系。实际上，主成分分析本身就是初始变量的线性组合。这样来看，也属于特征构造的，但是一般特征构造就是简单的四则运算。

上面呢就是简单说了一下，特征生成和特征构造，其实就是想尽各种办法产生个新的特征。下面呢，我们重点要说特征选择了，特征选择是非常重要的 ，如果特征选择失败，那么前面的工作都是徒劳的，大家试想一下，比如我们构造出了 100 多个特征，但是呢，却不知道哪个特征最重要，那不是还是没有解决问题吗，所以特征选择就显的尤为重要。

我们首先对特征选择的方法进行一个分类，从机器学习和统计方面进行一个分类，看看各自有哪些常用的算法。

我们先从统计的角度看一下，统计方面呢 ，我们最先想到的就是回归，回归是可以进行特征选择的，比如自变量 x 的回归系数如果是不显著的，那么我们就认为它不是一个好的特征。除了看显著性呢，还有常用的手段就是，先把所有的变量一起和 y 做一个回归，在逐渐去掉某些 x，观察模型的 deviance 如何变化，这类方法其实叫 Wrapper Methods。

但是呢，如果因变量 y 是离散的，那么我们的回归对应的就是广义线性回归模型了，那么这个时候还可以通过其他方法进行特征选择了，一般做法是单独将每个 x 和 y 做一个回归，完后再计算这个模型对应的基尼系数，通过观察基尼系数确定哪个方程对应的特征是最好的，但是呢，这种方法存在缺点，一个是每一个变量都需要单独和 y 做回归，比较麻烦。第二个是按照这种方法选出来的特征，其实效果不行，也就是在测试集上面表现并不好。那么呢，难道统计学方面就没有好一点方法吗，有呢，就是 lasso 回归，lasso 回归本来就是统计学大师搞出来的，现在已经发展出好多 lasso 回归的模型了。那么大家一看 lasso 这个单词是套索的意思。就是套着马脖子，主要是控制马的装置，那么在回归当中呢，主要是套回归系数的，意思是把回归系数控制住，不让它太大，本质上是一种正则化的手段，但是呢，不叫它太大，那数学的语言刻画方式有很多种了，但是 lasso 回归就选择了很巧妙的一种刻画方式，按照这种套路来，不仅可以约束系数，而且可以在模型最优的时候把不重要的系数约束为 0. 既然 x 的系数都成了 0 了，那我们也不用看显著性了，直接做到了特征选择，或者变量选择。目前看，这个方法是效果是非常好的，而且非常实用与高维数据分析。说的官方一些，这类方法叫 Embedded Methods，后面我们会专门讲 lasso。

下面呢，我们就从机器学习角度 看看，有没有相关的方法，当然是有的，我们最容易想到的就是回归数，或者叫决策树。这个方法好，主要是模型本身可解释性很强。它是按照 x 的值，对 y 进行了划分，划分的好坏依据是啥呢，主要是纯度，一个划分块里，纯度高，就说明划分的好，也就说明了这个划分变量选择的好。变量的重要性也就不言而喻了。当然这里是个简单的介绍，后面会详细地解读。实际上除了决策树，随机深林（random forest），bagging，boosting，gradient booting, 已经 xgboost 都有特征选择的功能，特别是 xgboost，这个算法很厉害，和 BGM 其实比较相似，后面我们会进行对比。除了基于树的模型呢，还有其他模型，比如神经网络，支持向量机也都有变量选择的功能。

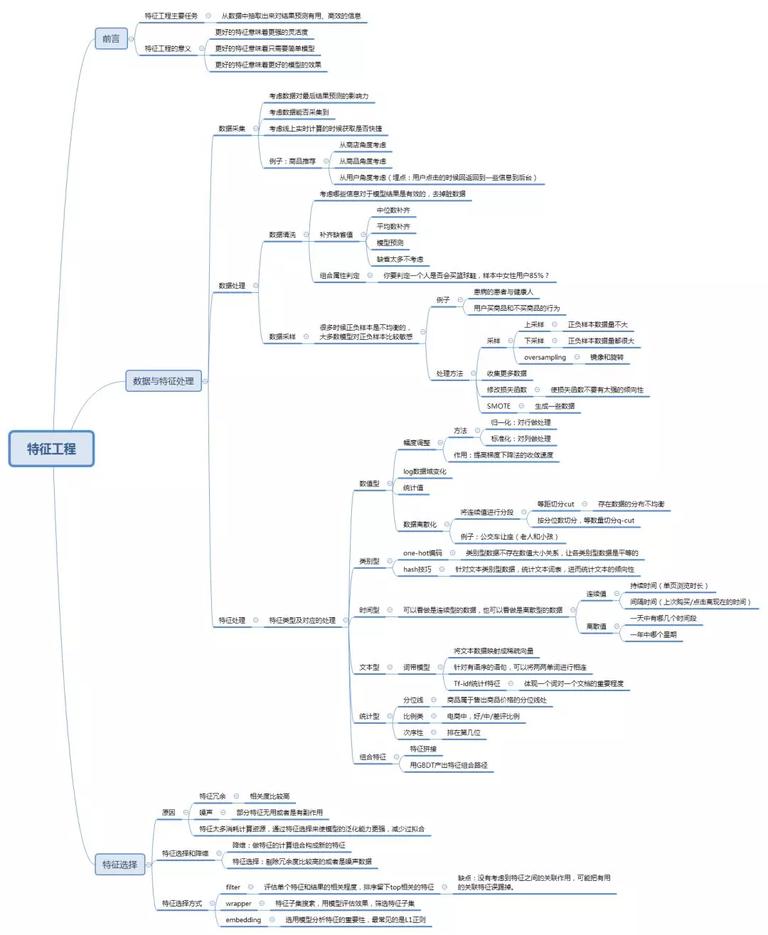
附特征工程完整任务图：