用Spark 来做大规模图形挖掘：第一部分

本教程分为两部分：

第一部分(也就是本篇啦!)： 用于无监督学习的图像

第二部分(点击这里)：如何使用神奇的图形力量，我们将会讨论一下标签的传播，Spark图形的帧和结果。下面的链接是样图和笔记的报告： https://github.com/wsuen/pygotham2018_graphmining

我也在PyGotham 2018上就这个话题发表了演讲：)

如果您是一名工程师，您很可能在完成搜索和查找算法时用过图形的数据结构。您是否也曾在机器学习问题上用过呢?

我们为什么需要关心图形?

对于数据科学家，图形是一个非常令人着迷的研究课题，标记数据的方法在处理机器学习问题并不总是有效。图形在无监督上下文中非常强大，因为它们通过利用数据的基础子结构来充分利用您拥有的数据。

对于某些机器学习问题，图形能帮您在没有标签的地方获得标记数据!

我将会向您介绍一种被称为社团检测(Community Detection)的方法去找到图形中同一类数据点的聚类。我们将使用Spark图形的帧数来处理我从2017年9月的Common Crawl dataset开始创建的大型网络图表。

 

 

图 101

图形的概念是用来表示对象配对关系的数据结构。图由节点(也成为顶点)和边组成。他们可以是定向的或者不定向。例如，Twitter可以是一个有向图;这种关系是单向的，仅仅是因为我关注另一个用户，不意味着他们也关注了我!

 

 

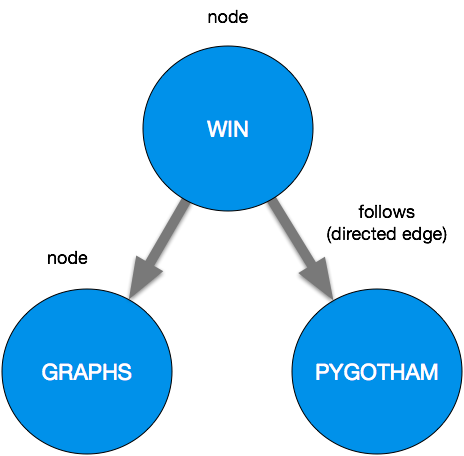
定向图的例子

当您为越来越多的页面执行此操作时，您会注意到子结构的出现。 在真实的网络数据上，这些子结构可能非常庞大和复杂!

为什么图形那么有用?

机器学习存在许多问题问题，其中标签(关于数据点是一类还是另一类的信息)不可用。 无监督学习问题依赖于在数据点之间找到相似性以将数据分类为组或群集。 将此与受监督的方法进行对比，其中数据用适当的类标记，并且您的模型学习使用这些标签来区分类。

 

 

源网址: http://beta.cambridgespark.com/courses/jpm/01-module.html

当您无法轻松获取更多数据时，无监督学习非常有用，因此您可以利用您拥有的数据获得更多价值。 标签可能不可用; 即使它们是，它们可能太耗时或昂贵。 在机器学习问题开始时，我们也可能不知道我们正在寻找多少类对象!

这就是我们在工具箱中需要图形的原因：

图形允许我们在无人监督的设置中从我们的数据中获得更多价值。 我们可以从图中获得聚类。

无人监督的学习与人类学习的方式没有什么不同。你是如何首先学会区分狗和猫的? 我想对于大多数人来说，没有人一生下来就会长大，还能用精确的分类术语来定义狗或猫是什么。你的父母也没有给你一张包含数千只猫狗照片的语料库，每张照片都标有标签，并要求你画出一个准确划分两类动物的决定边界。

如果你的童年和我的一样，你可能遇到了几只猫、几只狗。 一直以来，你确定了两种动物之间的显着差异，以及每种动物的相关共同特征。 我们的大脑在从我们的环境中吸收信息，综合这些数据，以及在我们生活中遇到的截然不同的事物之间制定共同点，我们的大脑实在是令人难以置信。

这是一个新闻网站下所有页面的示例图表。

聚类有许多令人激动的应用。我的工作中遇到了一些例子：

为无法通过标签学习的数据集预测标签
生成受众群体细分和分类分组
为类似的站点建立推荐人

发现异常

使用群集作为半监督机器学习集合的一部分。 群集可以帮助您将已知标签扩展到附近的数据点以增加训练数据大小，或者如果需要立即使用标签直到辅助系统对其进行分类，则可以直接使用它们。

这是最关键的：在无人监督的学习中，聚类是社团，反之亦然。

图形也是聚类!

唯一的区别是，您不依赖于工程特征，而是依赖图中的底层网络结构来派生集群。 您可以使用图中的边来测量数据点之间的相似度，而不是使用预定义的距离度量。

之前我们提到了社团(Community)，现在来大致介绍一下社团这个概念。社团定义不是唯一的，我们通常这样来描述它：一个社团是一个图的子结构，在这个子结构中，结构内的结点相互之间联系的比结构外的结点连的更近，更紧密。而找到这些社团(或者聚类)的过程叫做社团检测。

 

 

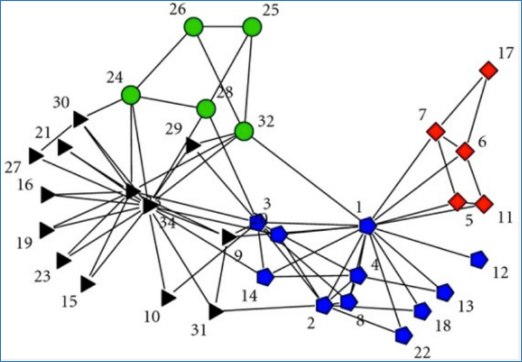
Zachary空手道俱乐部。图片来自于KONECT，2017年4月。数据集来自于1977年Zachary的最初研究。

Zachary空手道俱乐部数据集对一个跆拳道俱乐部中各种会员之间的关系进行了建模。有一次，俱乐部的两名成员发生冲突，俱乐部最终分裂成多个社区。由图可见，四个不同的社区由不同颜色表示。

可以思考一下无监督聚类算法是如何进行的。需要考虑到这一点，在你选择的特征空间中，其中的数据点与别的数据点之间的距离并不是特别紧密。数据之间的距离越紧密，也就意味着他们之间相似度越高。 你可以根据数据点之间的距离矩阵，将具有相似属性的数据放入同一个聚类中。

运用图可以帮助你实现类似的集群，而无需像传统集群那样选择数据特征。

每个浅蓝色点代表单个网页，即节点

每条深蓝色线代表两个页之间的链接，即边

 

 

新闻网站的子页面结构由我使用Gephi生成。

即使在此级别，您也可以看到页面的密集群集或社团。 您可以发现更高度中心性的节点(页面都具有链接到它们的大量其他页面)

如果一个站点的连接都如此密集，想象一下我们可以从成千上万的站点中挖掘出什么!

等等，为啥这种方法能行得通呢?

让我们继续往下学习。我们需要做出哪些假设，来让我们依靠社区检测来查找具有相似属性的节点?

最重要的一个是：

结点之间的连接线并不是随机的。

如果你的图是随机的话，那么根本不会行得通的。但是现实生活中大多数的图并不是随机的。结点相互之间的连接关系是存在某种相关性的。以下两个原则会解释其中的原因：

1.相互影响原则。相互连接在一起的结点更容易共享或者传递特征。试着想象一下，当你的几个朋友尝到了Spark带来的便利的时候，你作为与他们相互联系紧密的人，也有可能会开始学着使用Spark。“我所有的朋友都在用，所以我也要用”

2.同质相吸原则。结点之间有着一个相类似的特征，或者有某些关联的时候，很有可能会连接在一起。例如，如果你和我都喜欢用Python而且都喜欢图，用图来表示的话，我们很有可能是两个相互连接的结点。这也叫做正匹配，“物以类聚”。

在现实生活中，这两个原则会相互作用!

研究人员利用这些现象可以对图中的一些有趣的问题建模。例如，Farine et al通过动物之间强烈关联性预测了狒狒的位置——对行为生态学产生了很好的影响。

 

 

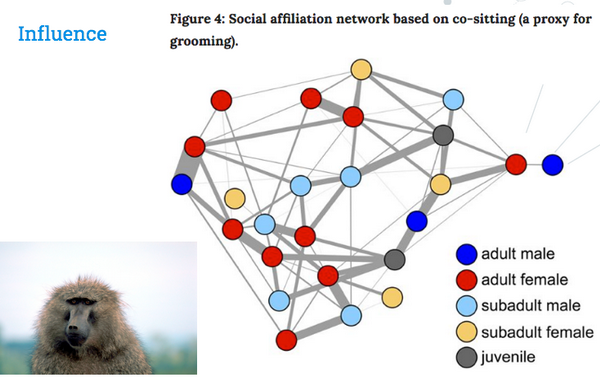
Farine, Damien R., et al“最近邻居和长期分支机构都能预测野生狒狒集体行动期间的个体位置。”科学报告6(2016)：27704

同质相吸原则经常用于社交网络研究。Adamic和Glance在2004年大选期间对政治博客进行了一项引人入胜的研究。 他们用图表的方式，显示了不同的博客如何相互引用;蓝色节点代表自由博客，红色节点是保守的博客。 也许不出所料，他们发现博客倾向于引用同样政治倾向的其他博客。

 

 

Adamic，Lada A.和Natalie Glance。 “政治博客圈和2004年美国大选：区分了他们的博客。”第三届国际链接发现研讨会论文集。ACM，2005年。

即使在个人层面上，同质相吸原则也是有道理的。 机会是你自己的朋友网络由可能与你年龄相同，住在同一个城镇，有相同的爱好，或去同一所学校的人组成! 在工作中，你是一个活生生同质相吸原则的例子。不要畏惧，大胆将它加入到简历中!

我们已经介绍了图是怎么运用数据中基本的网络特性来生成聚类。在互联网中，这些聚类对于推荐系统、观众分类、以及异常检测等等都有重大意义。

在第二部分(链接传送门)，我们会将对社团检测技术进行深入研究，并且学着怎么利用常用的爬虫数据集，从网页的图状结构中得到聚类。

鸣谢

首先感谢Yana Volkovich博士对我图论的学习与深入研究的大力帮助，您是一名很棒的导师。然后感谢那些对于我演讲，提供了反馈信息的同事们。

参考文献

Adamic, Lada A., and Natalie Glance. “The political blogosphere and the 2004 US election: divided they blog.” Proceedings of the 3rd international workshop on Link discovery. ACM, 2005.

Common Crawl dataset (September 2017).

Farine, Damien R., et al. “Both nearest neighbours and long-term affiliates predict individual locations during collective movement in wild baboons.” Scientific reports 6 (2016): 27704

Fortunato, Santo. “Community detection in graphs.” Physics reports 486.3–5 (2010): 75–174.

Girvan, Michelle, and Mark EJ Newman. “Community structure in social and biological networks.” Proceedings of the national academy of sciences 99.12 (2002): 7821–7826.

Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. Mining of massive datasets. Cambridge University Press, 2014.

Raghavan, Usha Nandini, Réka Albert, and Soundar Kumara. “Near linear time algorithm to detect community structures in large-scale networks.” Physical review E 76.3 (2007): 036106.

Zachary karate club network dataset — KONECT, April 2017.

时间:2018-11-11 23:05  来源:    转发量:次