常见数据结构和Javascript实现总结
做前端的同学不少都是自学成才或者半路出家,计算机基础的知识比较薄弱,尤其是数据结构和算法这块,所以今天整理了一下常见的数据结构和对应的Javascript的实现,希望能帮助大家完善这方面的知识体系。
1. Stack(栈)

Stack的特点是后进先出(last in first out)。生活中常见的Stack的例子比如一摞书,你最后放上去的那本你之后会最先拿走;又比如浏览器的访问历史,当点击返回按钮,最后访问的网站最先从历史记录中弹出。
Stack一般具备以下方法:
push:将一个元素推入栈顶
pop:移除栈顶元素,并返回被移除的元素
peek:返回栈顶元素
length:返回栈中元素的个数
Javascript的Array天生具备了Stack的特性,但我们也可以从头实现一个 Stack类:
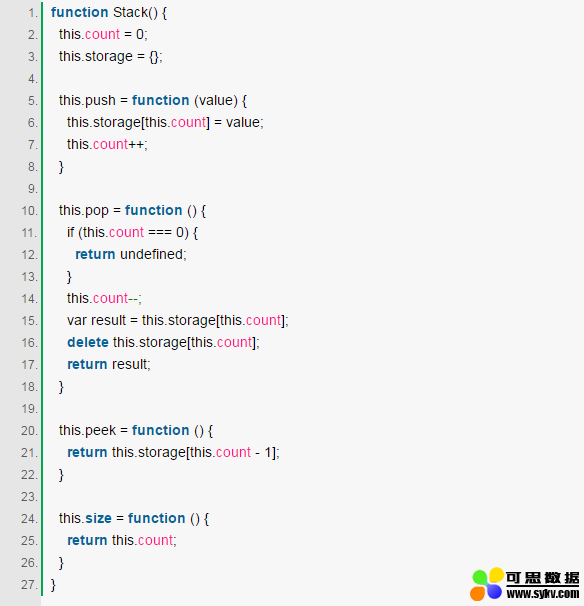
2. Queue(队列)

Queue和Stack有一些类似,不同的是Stack是先进后出,而Queue是先进先出。Queue在生活中的例子比如排队上公交,排在第一个的总是最先上车;又比如打印机的打印队列,排在前面的最先打印。
Queue一般具有以下常见方法:
enqueue:入列,向队列尾部增加一个元素
dequeue:出列,移除队列头部的一个元素并返回被移除的元素
front:获取队列的第一个元素
isEmpty:判断队列是否为空
size:获取队列中元素的个数
Javascript中的Array已经具备了Queue的一些特性,所以我们可以借助Array实现一个Queue类型:

Priority Queue(优先队列)
Queue还有个升级版本,给每个元素赋予优先级,优先级高的元素入列时将排到低优先级元素之前。区别主要是enqueue方法的实现:
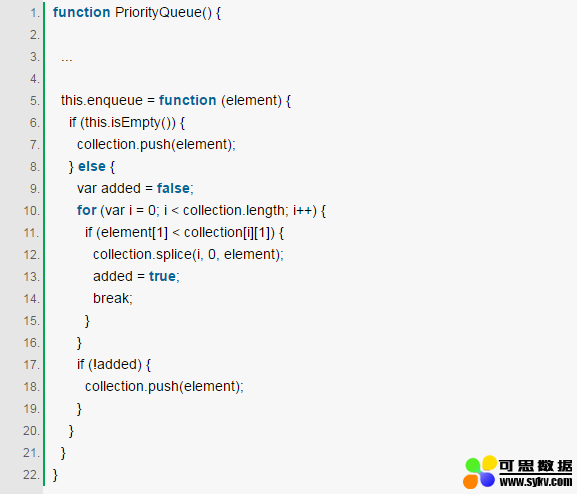
测试一下:
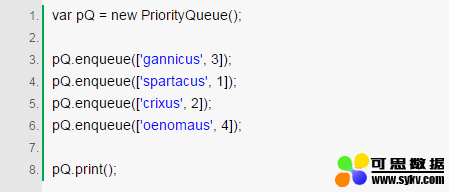
结果:

3. Linked List(链表)
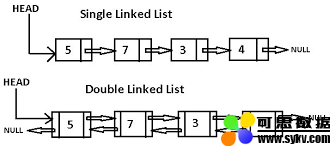
顾名思义,链表是一种链式数据结构,链上的每个节点包含两种信息:节点本身的数据和指向下一个节点的指针。链表和传统的数组都是线性的数据结构,存储的都是一个序列的数据,但也有很多区别,如下表:
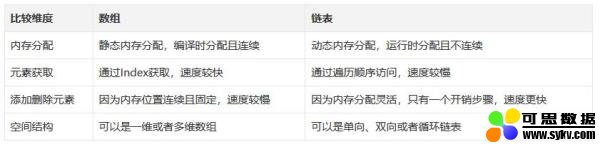
一个单向链表通常具有以下方法:
size:返回链表中节点的个数
head:返回链表中的头部元素
add:向链表尾部增加一个节点
remove:删除某个节点
indexOf:返回某个节点的index
elementAt:返回某个index处的节点
addAt:在某个index处插入一个节点
removeAt:删除某个index处的节点
单向链表的Javascript实现:
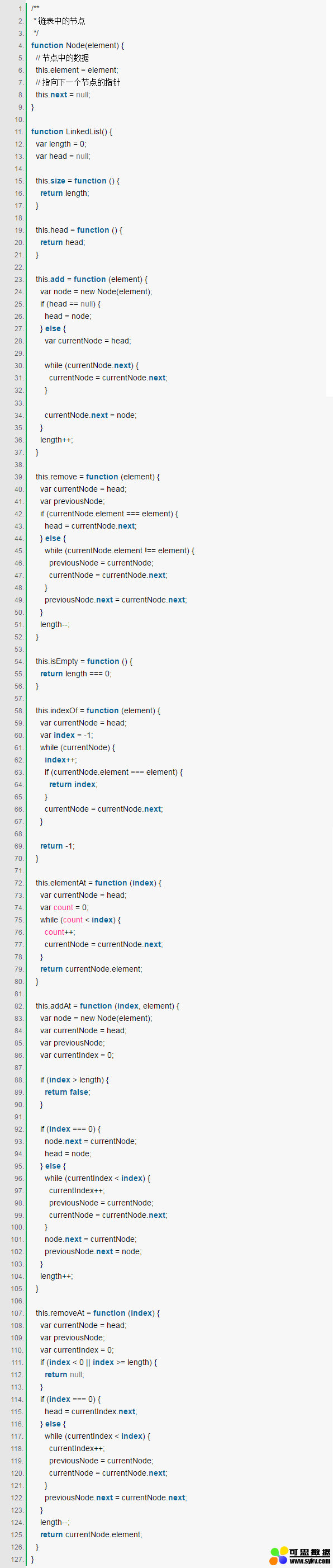
4. Set(集合)
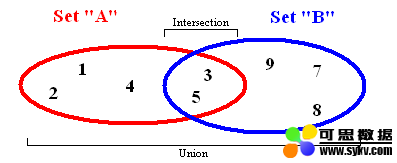
集合是数学中的一个基本概念,表示具有某种特性的对象汇总成的集体。在ES6中也引入了集合类型Set,Set和Array有一定程度的相似,不同的是Set中不允许出现重复的元素而且是无序的。
一个典型的Set应该具有以下方法:
values:返回集合中的所有元素
size:返回集合中元素的个数
has:判断集合中是否存在某个元素
add:向集合中添加元素
remove:从集合中移除某个元素
union:返回两个集合的并集
intersection:返回两个集合的交集
difference:返回两个集合的差集
subset:判断一个集合是否为另一个集合的子集
使用Javascript可以将Set进行如下实现,为了区别于ES6中的Set命名为MySet:
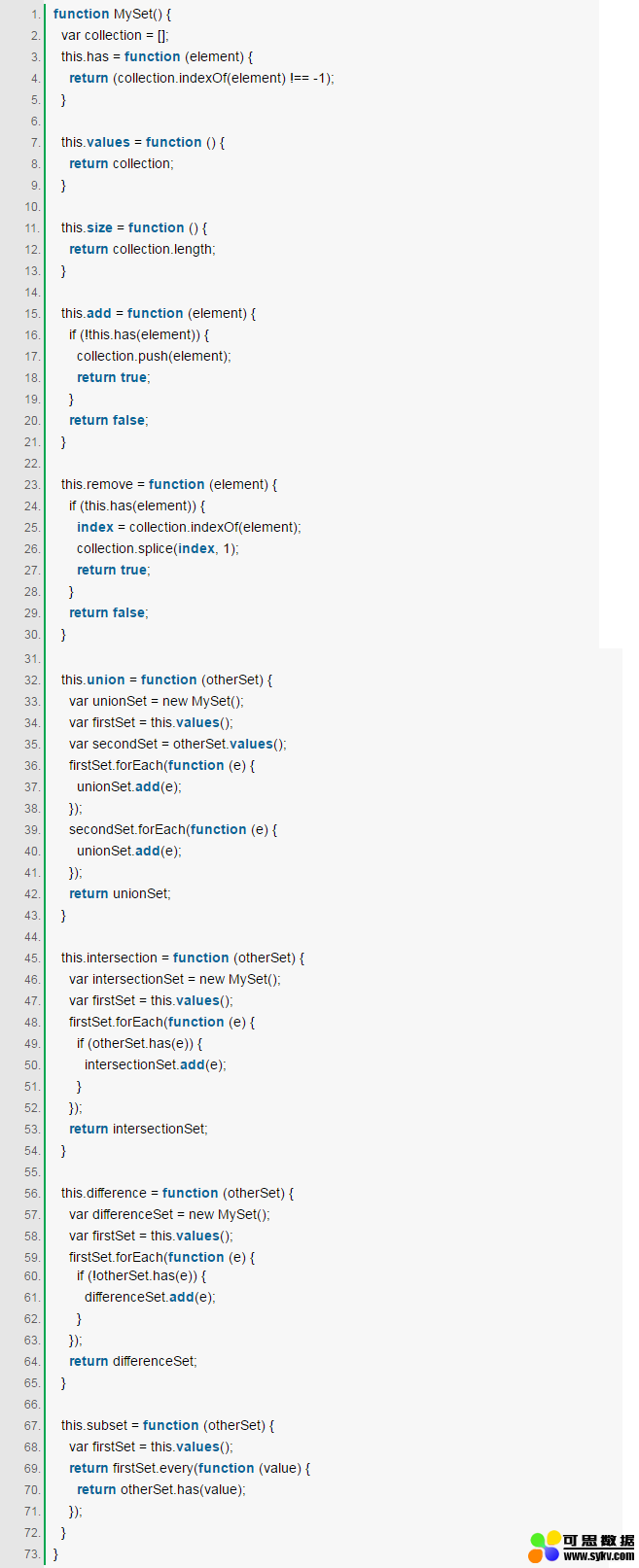
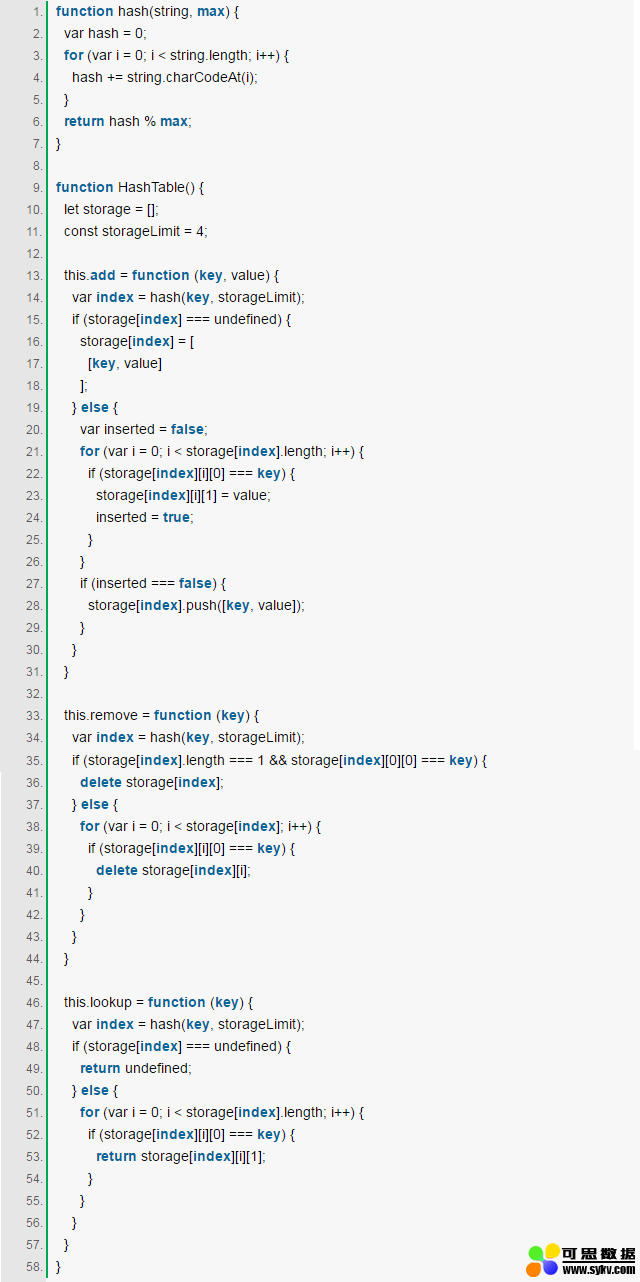
5. Hash Table(哈希表/散列表)

Hash Table是一种用于存储键值对(key value pair)的数据结构,因为Hash Table根据key查询value的速度很快,所以它常用于实现Map、Dictinary、Object等数据结构。如上图所示,Hash Table内部使用一个hash函数将传入的键转换成一串数字,而这串数字将作为键值对实际的key,通过这个key查询对应的value非常快,时间复杂度将达到O(1)。Hash函数要求相同输入对应的输出必须相等,而不同输入对应的输出必须不等,相当于对每对数据打上唯一的指纹。
一个Hash Table通常具有下列方法:
add:增加一组键值对
remove:删除一组键值对
lookup:查找一个键对应的值
一个简易版本的Hash Table的Javascript实现:
6. Tree(树)
顾名思义,Tree的数据结构和自然界中的树极其相似,有根、树枝、叶子,如上图所示。Tree是一种多层数据结构,与Array、Stack、Queue相比是一种非线性的数据结构,在进行插入和搜索操作时很高效。在描述一个Tree时经常会用到下列概念:
Root(根):代表树的根节点,根节点没有父节点
Parent Node(父节点):一个节点的直接上级节点,只有一个
Child Node(子节点):一个节点的直接下级节点,可能有多个
Siblings(兄弟节点):具有相同父节点的节点
Leaf(叶节点):没有子节点的节点
Edge(边):两个节点之间的连接线
Path(路径):从源节点到目标节点的连续边
Height of Node(节点的高度):表示节点与叶节点之间的最长路径上边的个数
Height of Tree(树的高度):即根节点的高度
Depth of Node(节点的深度):表示从根节点到该节点的边的个数
Degree of Node(节点的度):表示子节点的个数
我们以二叉查找树为例,展示树在Javascript中的实现。在二叉查找树中,即每个节点最多只有两个子节点,而左侧子节点小于当前节点,而右侧子节点大于当前节点,如图所示:
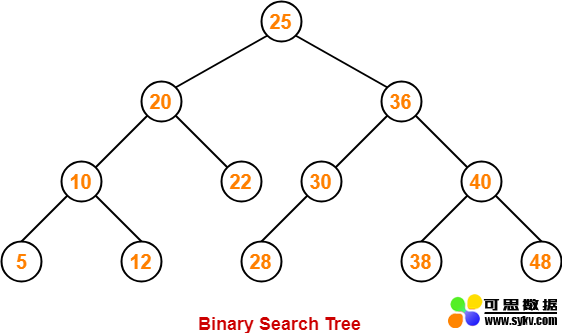
一个二叉查找树应该具有以下常用方法:
add:向树中插入一个节点
findMin:查找树中最小的节点
findMax:查找树中最大的节点
find:查找树中的某个节点
isPresent:判断某个节点在树中是否存在
remove:移除树中的某个节点
以下是二叉查找树的Javascript实现:
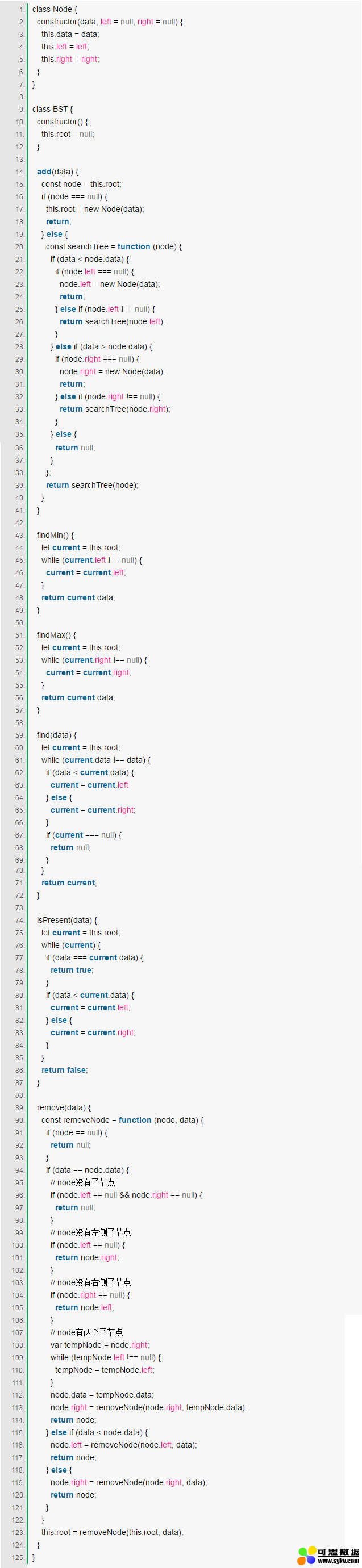
测试一下:

打印结果:

7. Trie(字典树,读音同try)
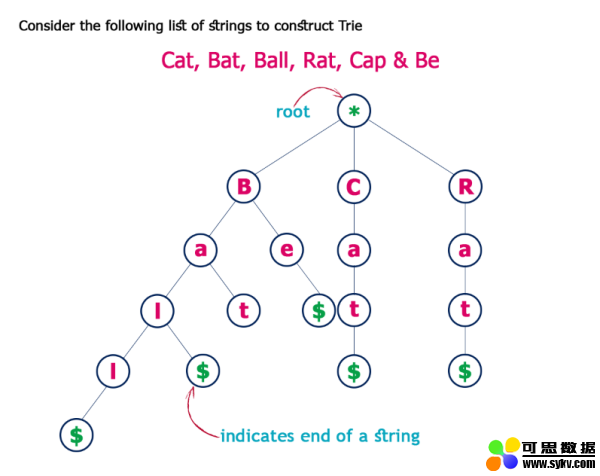
Trie也可以叫做Prefix Tree(前缀树),也是一种搜索树。Trie分步骤存储数据,树中的每个节点代表一个步骤,trie常用于存储单词以便快速查找,比如实现单词的自动完成功能。 Trie中的每个节点都包含一个单词的字母,跟着树的分支可以可以拼写出一个完整的单词,每个节点还包含一个布尔值表示该节点是否是单词的最后一个字母。
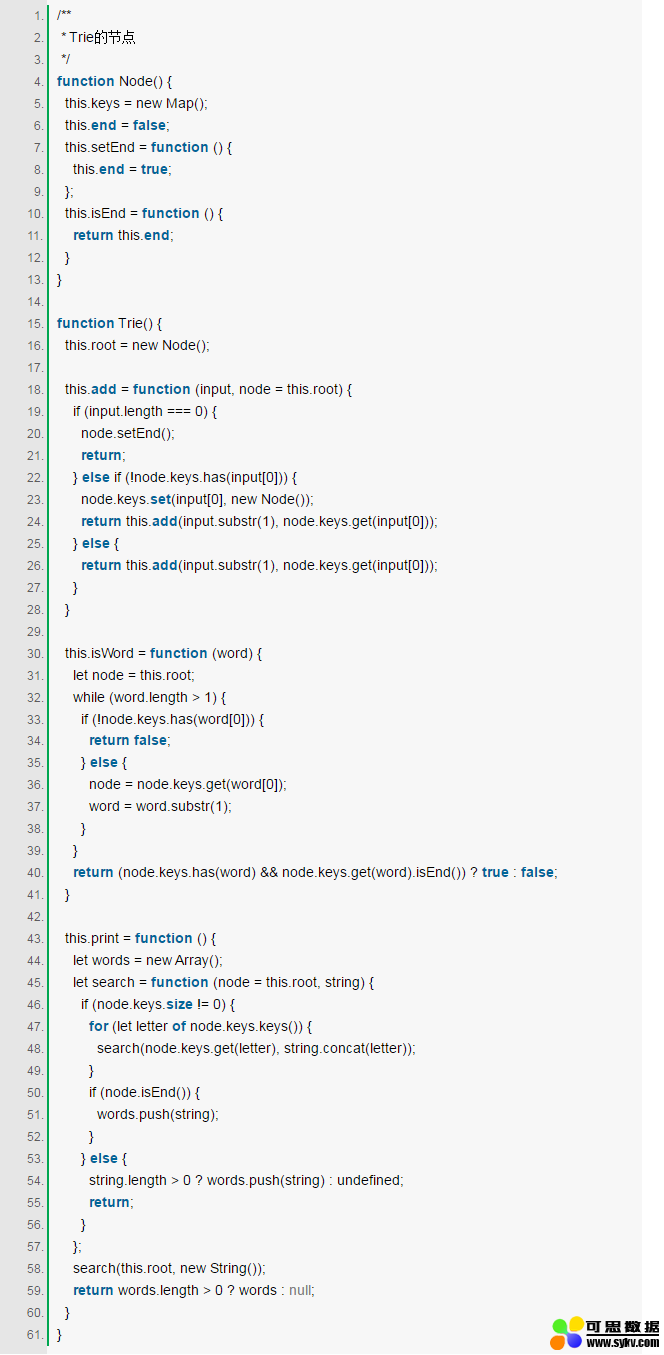
Trie一般有以下方法:
add:向字典树中增加一个单词
isWord:判断字典树中是否包含某个单词
print:返回字典树中的所有单词
8. Graph(图)
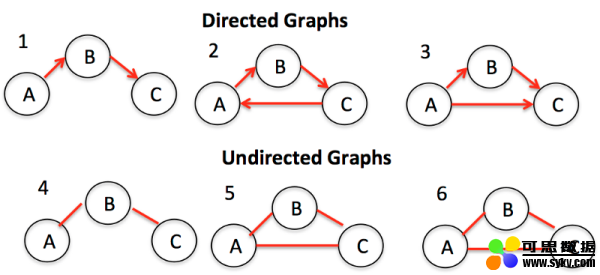
Graph是节点(或顶点)以及它们之间的连接(或边)的集合。Graph也可以称为Network(网络)。根据节点之间的连接是否有方向又可以分为Directed Graph(有向图)和Undrected Graph(无向图)。Graph在实际生活中有很多用途,比如:导航软件计算最佳路径,社交软件进行好友推荐等等。
Graph通常有两种表达方式:
Adjaceny List(邻接列表):
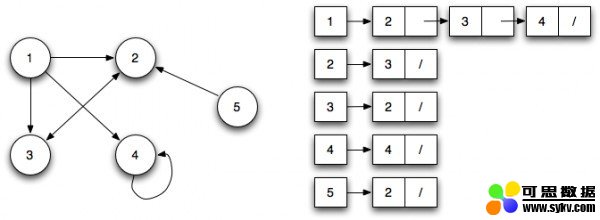
邻接列表可以表示为左侧是节点的列表,右侧列出它所连接的所有其他节点。
和 Adjacency Matrix(邻接矩阵):
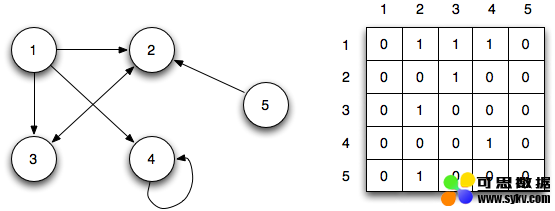
邻接矩阵用矩阵来表示节点之间的连接关系,每行或者每列表示一个节点,行和列的交叉处的数字表示节点之间的关系:0表示没用连接,1表示有连接,大于1表示不同的权重。
访问Graph中的节点需要使用遍历算法,遍历算法又分为广度优先和深度优先,主要用于确定目标节点和根节点之间的距离,
在Javascript中,Graph可以用一个矩阵(二维数组)表示,广度优先搜索算法可以实现如下:

测试一下:

打印:

最后,推荐大家使用Fundebug,一款很好用的BUG监控工具~
本文旨在向广大前端同学普及常见的数据结构,本人对这一领域也只是初窥门径,说的有差池的地方欢迎指出。也希望大家能打牢基础,在这条路上走的更高更远!
作者:MudOnTire来源:SegmentFault.com

时间:2019-08-14 14:20 来源: 转发量:次
声明:本站部分作品是由网友自主投稿和发布、编辑整理上传,对此类作品本站仅提供交流平台,转载的目的在于传递更多信息及用于网络分享,并不代表本站赞同其观点和对其真实性负责,不为其版权负责。如果您发现网站上有侵犯您的知识产权的作品,请与我们取得联系,我们会及时修改或删除。
相关文章:
相关推荐:
网友评论:
















