一份数据科学“必备”的数学基础清单

秋招已经开始，相信很多同学想从事。对于而言，数学知识的储备重要吗？答案显而易见，掌握好数学对于从事该岗位而言是很重要的。数学一直是任何当代科学学科的基础，几乎所有的现代（包括所有的）都有一些深刻的数学知识。在本文中，我们将讨论想成为一名优秀的应该掌握的基本数学知识，以便在各个方面都能很好地适应。

 

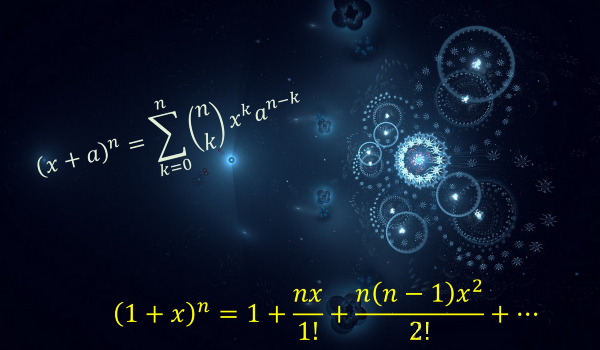
介绍

有时候，作为一名数据科学家（甚至是团队的初级分析师），你必须全心全意地学习那些基础的数学知识，或者正确地应用这些技术，有时候你可以通过使用一些API或者拿来即用的算法完成相关任务。

但是，如果你对用于为用户创建有意义的产品推荐算法背后的数学知识有充分的了解，这将永远不会对你有任何损害。通常情况下，懂得这些知识应该能让你在同龄人中占有一席之地。

毫无疑问，想成为一名顶级的数据科学家还需要掌握其他领域的知识，比如编程能力、具有一定的商业头脑，以及对数据的独特分析和好奇心态。本文所要做的就是整理一份最基本的数学技能指南，以帮助你更好地完成这项工作。
 

对“新手”特别重要

对于那些在其他领域花费大量时间并想进入这一领域的专业人士来说，基础学知识显得尤其重要，比如硬件工程、零售、化学加工工业、企业管理等领域。

虽然这些领域的工作中也涉及电子表格、数值计算和预测方面的内容，但在数据科学实践中对必要的数学技能要求却大不相同。
 

为什么以及如何与众不同——这是科学而不是数据

考虑一个Web开发人员（或业务分析师），他可能每天需要处理大量的数据和信息，但可能没有强调对该数据进行建模。通常，数据分析的任务重点在于“ 根据需求利用数据并继续推进项目 ”，而不是深入探索，数据科学应该始终关注科学（而不是数据），其中大多数是科学处理过程的特点：
 

• 通过探测潜在的动态来建模过程
• 构建假设
• 严格评估数据源的质量
• 量化数据和预测的不确定性
• 培养个人从信息流中识别隐藏模式的感觉
• 清楚地了解模型的局限性
• 理解数学证明及其背后的所有抽象逻辑

这类的培训，大多数没有考虑正数而是讲解抽象的数学实体（及其属性和相互关系），被认为是四年制大学学位课程标准课程的一部分。个人不需要以优异的成绩从顶尖大学毕业来获得这种水平的数学知识，但不幸的是，过去的访问量几乎在变少。
 

展示成功的蓝图

一般而言，没有通用的蓝图。就其本质而言，数据科学并不依赖于特定的学科领域，并且可能是在单个项目中处理各种现象，如癌症诊断和社会行为分析等，这会产生各种令人眼花缭乱的n维数学对象、统计分布、优化目标函数等。

上面提到的那些东西是什么？如果你对其补熟悉的话，以下是我们需要学习、吸收的内容建议。
 

函数、变量、方程、图

 

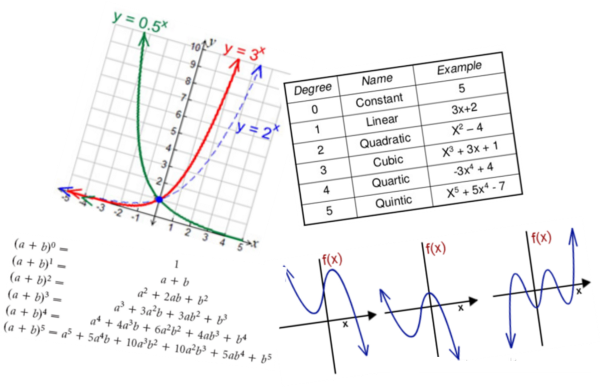
What：从基本的知识开始，如线的方程式到二项式定理及其性质。

• 对数、指数、多项式函数、有理数
• 基本几何和定理，三角恒等式
• 实数和复数的基本属性
• 级数、总和和不等式
• 图表和绘图、笛卡尔和极坐标系统、圆锥曲线

示例：如果想了解在排序后在百万项目数据库上搜索的运行速度，你将会遇到二进制搜索的概念。为了理解它的行为，需要理解对数和递推方程。或者是分析时间序列的话，可能会遇到周期函数和指数衰减等概念。

学习资源：

•  
•  
•  

统计

 

What：成长为数据科学家必须知道的知识。在关于数据科学的讨论中，再如何强调掌握统计和概率的基本概念的重要性都不为过。该领域的许多从业者实际上称经典机器学习（非神经网络）只是统计学习。该主题内容非常广泛，重点规划大多数的基本概念即可。

• 数据摘要和描述性统计、集中趋势、方差、协方差及相关性
• 基本概率：基本概念、期望、概率演算、贝叶斯定理、条件概率
• 概率分布函数：均匀、标准、二项式、卡方、学生t分布、中心极限定理、
  采样、测量、错误、随机数生成
• 假设检验、A / B检验、置信区间、p值，
• 方差分析、t检验
• 线性回归，正则化

示例：在面试时，作为一名潜在的数据科学家，如果你能掌握上面提到的所有概念，你会很快地给对方留下深刻的印象。作为数据科学家，你几乎每天都会使用上述中的一些概念。

学习资源：

•  
•  
•  

线性代数

 

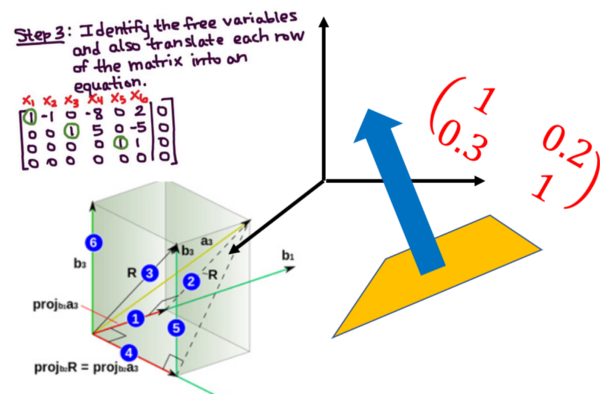
What：社交网络软件上的朋友推荐、音乐APP中的歌曲推荐以及使用深度迁移学习将自拍照转换为其它风格的图像，这些都有用到线性代数的知识。线性代数是数学领域的一个重要分支，用于理解大多数机器学习算法如何在数据流上工作以创建洞察力。以下是要学习的基本内容：

• 矩阵和向量的基本属性——标量乘法、线性变换、转置、共轭、秩、行列式
• 内积外积、矩阵乘法法则和各种算法、逆矩阵
• 特殊矩阵——方阵、单位矩阵、三角矩阵、稀疏和密集矩阵、单位向量、对称矩阵、埃尔米特矩阵、斜埃尔米特矩阵和酉矩阵，
• 矩阵分解、高斯/高斯-若尔消除法，求解Ax = b方程的线性系统
• 矢量空间、基、跨度、正交性、线性最小二乘，
• 特征值、特征向量和对角化，奇异值分解（SVD）

示例：如果你使用过主成分分析（PCA）降维技术，那么你可能已经使用过奇异值分解来实现数据集的紧凑维度表示，使得参数更少。所有神经网络算法都使用线性代数技术来表示和处理网络结构和学习操作。

学习资源：

•  
•  

微积分

 

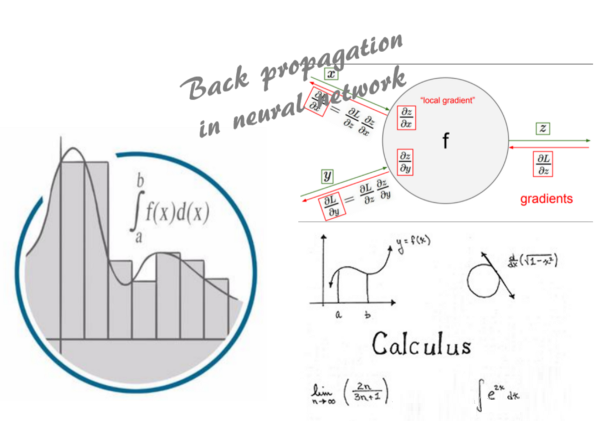
What：无论你在大学期间喜欢它还是讨厌它，在数据科学或机器学习领域的许多地方都会应用微积分的概念。它隐藏在线性回归中最小二乘问题的简单分析解决方案背后，或者嵌入到神经网络学习新模式的每个反向传播中。以下是要学习的内容：

• 单变量、极限、连续性和可微性的函数
• 中值定理、不确定性和洛必达法则
• 极大值和极小值
• 乘积和链式法则
• 泰勒级数、无穷级数求和/积
• 积分计算和中值定理、对有限和不正确积分的评价，
• Beta和Gamma函数
• 多变量函数、极限、连续性、偏导数
• 普通和偏微分方程的基础知识

示例：如何实现逻辑回归算法，它很有可能使用一种称为“梯度下降”的方法来找到最小损失函数。要了解其如何工作，需要使用来自微积分的基本概念——梯度、导数、极限和链式法则。

学习资源：

•  
•  
•  

离散数学

 

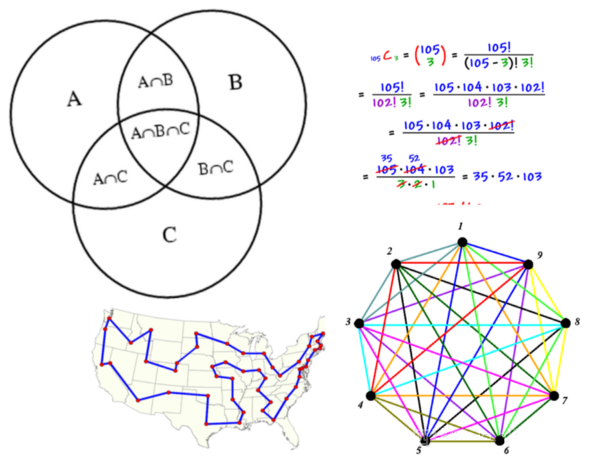
What：这部分内容通常是“数据科学数学”方案中较少讨论的主题，但事实是所有现代数据科学都是在计算系统的帮助下完成的，离散数学是这类系统的核心。要学习的内容：

• 集合、子集和幂集
• 计数函数、组合学、可数性
• 基本证明技术——归纳法、反证法
• 归纳、演绎和命题逻辑的基础知识
• 基本数据结构——堆栈、队列、图、数组、哈希表、树
• 图表属性——连接组件、度、最大流量/最小切割概念、图形着色
• 递归关系和方程
• 函数的增长和O(n)符号概念

示例：在任何社交网络分析中，你需要知道图的属性和快速算法以搜索和遍历整个网络。在选择任何算法时，都需要通过使用 O(n)表示法来了解时间和空间复杂度。

学习资源：

•  
•  
•  

最优化、运筹学

 

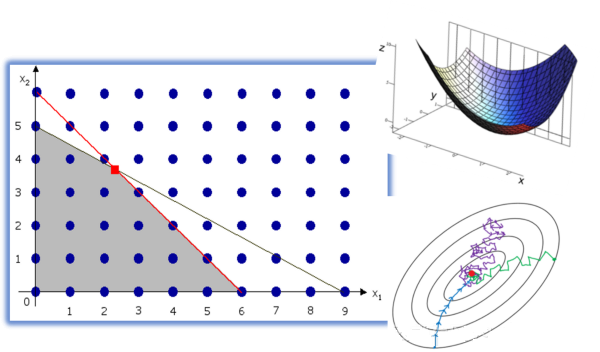
What：这些主题与应用数学中的传统话语没什么不同，因为它们在专业领域——理论计算机科学、控制理论或运筹学中最为相关和最广泛使用。实际上，每种机器学习算法旨在最小化受各种约束影响的某种估计误差，这就是优化问题。要学习的内容：

• 优化的基础——如何制定问题
• 最大值、最小值、凸函数、全局解
• 线性规划、单纯形算法
• 整数规划
• 约束编程、背包问题

示例：使用最小平方损失函数的简单线性回归问题通常具有精确的解析解，但逻辑回归问题却没有，要理解其中的原因，需要了解优化中凸性的概念，这也将阐明为什么我们必须对大多数机器学习问题中的“近似”解决方案能够满意。

资源：

•  
•  
•  

与此主题相关的一些优秀文章

•  
•  
•  
•  
•  

结束语

作为一名数据科学家，需要掌握这么多的知识，看起来似乎有些让人绝望，但你不需要感到害怕，网络上资源很多，可以根据个人需求定制自己的学习资源列表。在复习这些知识并学习新概念之后，个人能力会有很大的提升，这是成为数据科学家的一大飞跃。
 

作者：Tirthajyoti Sarkar，数据科学家

文章原标题《》，译者：海棠
 

时间:2018-08-20 23:22  来源:    转发量:次