一份关于如何为回归任务选择机器学习算法指南

当遇到任何类型的机器学习(ML)问题时，可能会有许多不同的算法可供你选择。但是在机器学习中，有一个“没有免费午餐”的定理，该定理表明，基本上没有一种机器学习算法能够对所有问题而言是最合适的。不同机器学习算法的性能很大程度上取决于数据的大小和结构。因此，除非我们直接通过一次次实验和错误来测试我们采取的算法，否则，如何选择正确的算法通常仍然是不清楚的。

事物总有两面性，每种机器算法也会有一些优点和缺点，我们可以根据其优点和缺点作为选择合适算法的一种指导。虽然一种具体的算法并不总是优于另外一种算法，但我们可以根据每种算法本身具有的一些属性作为快速选择正确算法和调整超参数的指南。本文将分析一些针对回归问题的典型机器算法，并根据其优势和劣势制定何时使用它们的规则。看完这篇文章，应该可以帮助你为回归问题选择出最佳的机器算法!

线性和多项式回归

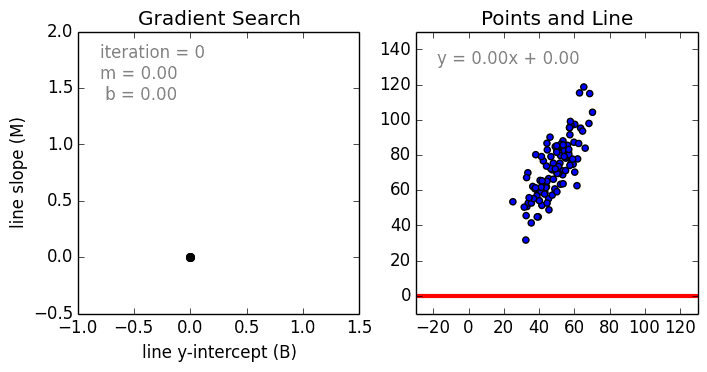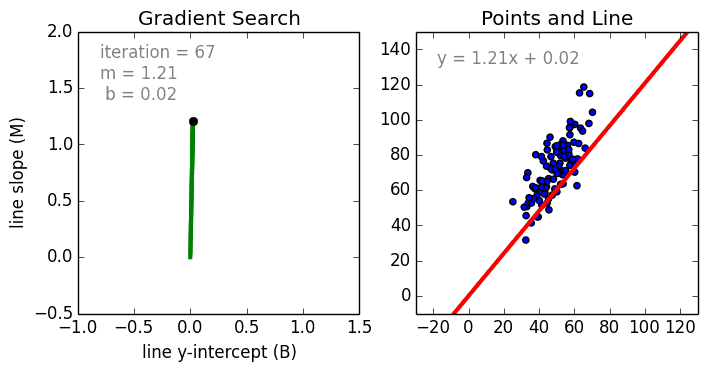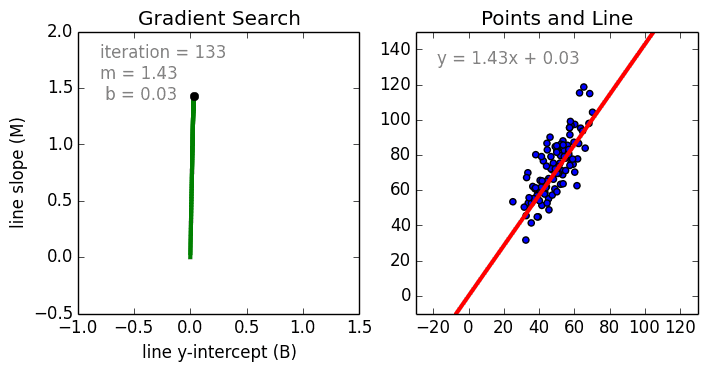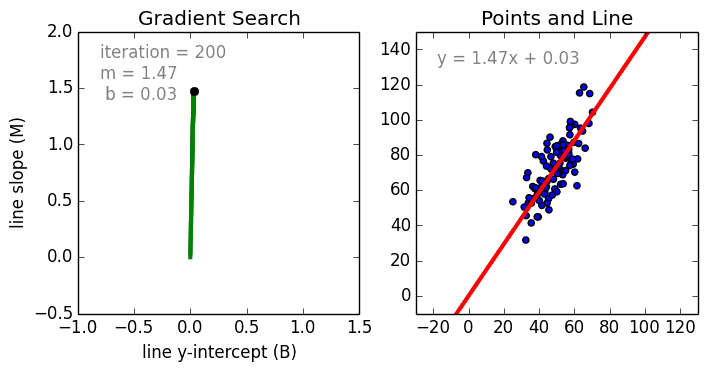
线性回归

从简单的情况开始讲解，单变量线性回归是一种技术，用于使用线性模型对单个输入自变量(特征变量)和输出因变量之间的关系进行建模。更一般的情况是多变量线性回归，其中为多个独立输入变量(特征变量)和输出因变量之间的关系构建模型。该模型保持线性，因为输出是输入变量的线性组合。

存在第三种最常见的情况被称为多项式回归，其中模型变为特征变量的非线性组合，即等式中可以存在指数变量、正弦项和余弦项等。然而，这种情况需要知道数据如何与输出相关，可以使用随机梯度下降(SGD)算法训练回归模型。

优点

能够快速建模，且当要建模的关系不是非常复杂并且没有大量数据时，该方法特别有用。

线性回归很容易被理解，这对于业务决策而言显得非常有价值。

缺点

对于非线性数据，多项式回归在设计时可能非常具有挑战性，因为必须具有关于数据结构和特征变量之间关系的一些信息。

由于上述原因，当涉及高度复杂的数据时，这类模型不如其它模型好。

神经网络

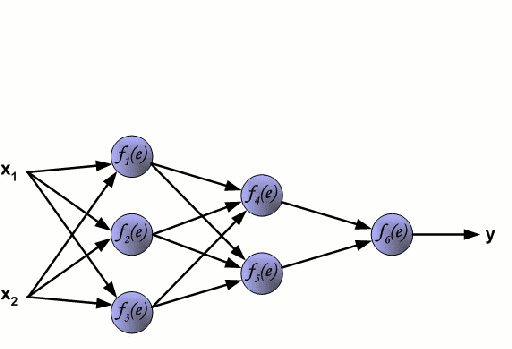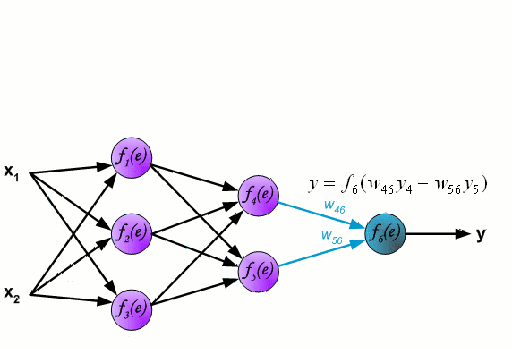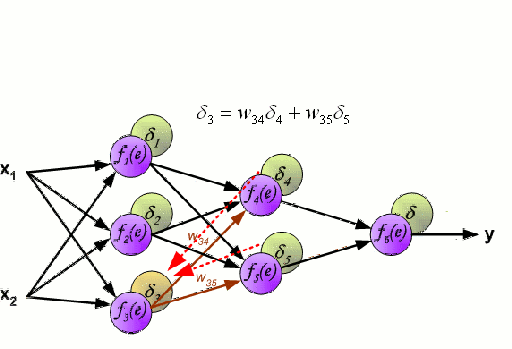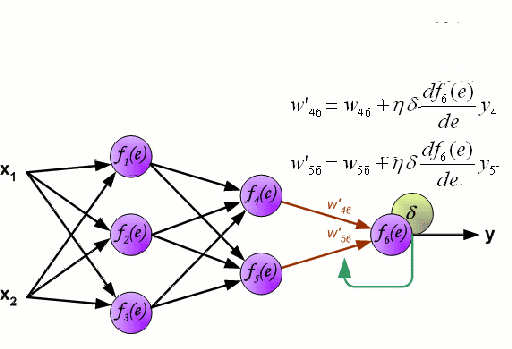
神经网络

神经网络由一组称为神经元的节点相互连接组成。来自数据的输入特征变量作为多变量线性组合传递给这些神经元，其中乘以每个特征变量的值称为权重。然后将非线性应用于该线性组合，这给予神经网络模拟复杂非线性关系的能力。神经网络可以具有多层结构，每一层的输出出以相同的方式传递给下一层。在最后的一层，即输出端，通常不应用非线性。一般使用随机梯度下降(SGD)和反向传播算法训练神经网络模型(如上图所示)。

优点

由于神经网络可以有许多具有非线性的隐藏层，因此它们对于高度复杂的非线性关系建模方面非常有效。

通常，我们不必担心神经网络中的数据结构，该方法在对任何类型特征变量关系学习时都非常灵活。

研究表明，简单地为网络提供更多的训练数据，无论是全新的数据，还是增加原始数据集，都有利于提升网络的性能。

缺点

由于这类模型的复杂性，它们不易于解释和理解。

它们在训练时可能具有一定的挑战性，且对计算性能有一定的要求，需要仔细的调整超参数和学习速率的设置。

神经网络方法一般需要大量数据才能获得高的性能，并且在“小数据”情况下通常优于其他的机器算法。

回归树和随机森林

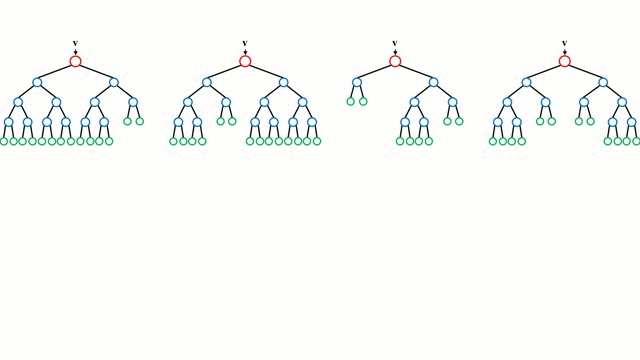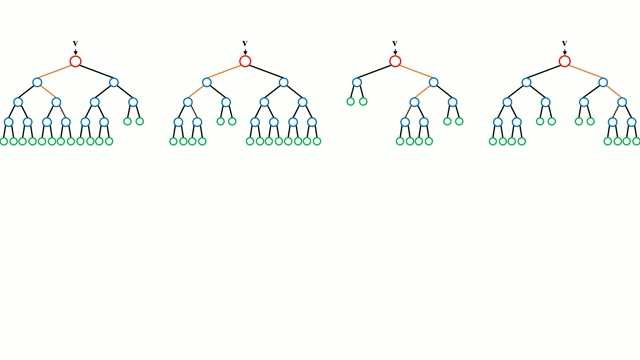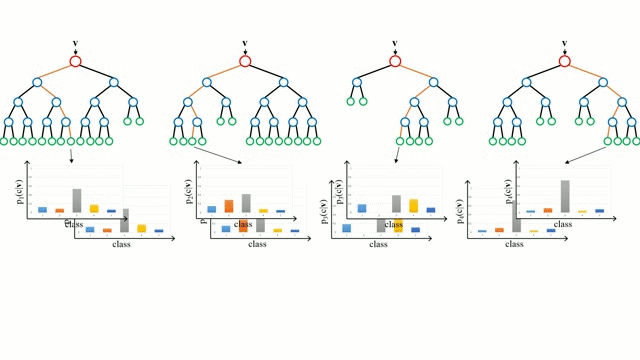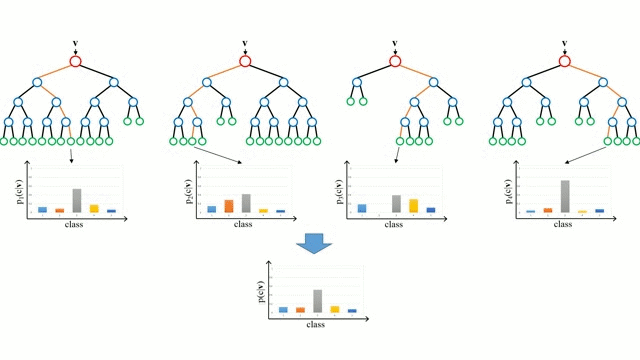
随机森林

从基本情况开始说起，决策树是一种直观的模型，遍历树的分支，并根据节点的决定来选择下一个分支。树形导入是将一组训练实例作为输入，决定哪些属性是最佳分割，分割数据集以及在生成的分割数据集上重复操作，直到所有训练实例都被分类务。在构建决策树时，目标是分割创建最纯子节点的属性，这将使我们的数据集中的所有实例分类所需的分割数量保持最小。纯度是通过信息增益的概念来衡量的，信息增益的概念与先前看不见的实例需要了解多少以便对其进行适当分类有关。在实践中，一般是通过比较熵，或者如果要在给定属性上进一步对当前数据集分区进行分区，则对单个实例进行分类的信息量。

随机森林只是决策树的集合，输入向量通过多个决策树运行。对于回归问题，所有树的输出值是取的平均值;对于分类问题，投票方案用于确定最终类别。

优点：

擅长学习复杂、高度非线性的关系。通常可以实现相当高的性能，优于多项式回归，并且性能通常与神经网络相当。

很容易被理解和理解。虽然最终训练的模型可以学习到复杂的关系，但是在训练期间建立的决策边界很容易理解。

缺点：

由于在决策树训练时，可能很容易出现严重的过度拟合现象。完整的决策树模型可能过于复杂并且包含不必要的结构，这种情况下有时可以通过适当的树枝修剪和更大的随机森林集合来缓解。

使用较大的随机森林集合来实现更高的性能，这会使得训练过程耗时长，且需要更多的内存。

结论

本文总结了一些针对于回归问题的机器学习方法，辩证地分析了其各自的优缺点。可以根据具体问题选择合适的机器学习算法以完成相应的任务。