AI产品经理需要了解的微积分通识

前两篇笔者分别为大家介绍了AI产品经理需要了解的概率论通识和线性代数通识，本篇文章中，笔者将继续为你介绍AI产品经理需要了解的微积分通识，供大家一参考学习。

1665年，牛顿从剑桥大学毕业了，英国爆发瘟疫，学校关闭，牛顿回到家乡躲避瘟疫，在家乡牛顿被苹果砸了一下，发明了流数法、发现了色散，并提出了万有引力定律。

牛顿当时提出的流数法，就是我们所说的微积分。但是牛顿当时并没有把它看得太重，只是把它作为数学工具，是自己研究物理问题时的副产品，也没有把这种方法公之于众。

十年之后，莱布尼茨了解到牛顿的数学工作并在1684年，连续发表了两篇论文，正式提出了微积分的思想，牛顿得知后通过英国皇家科学院公开指责莱布尼茨，没有提及自己，于是之后在谈到微积分公式，我们称之为“牛顿-莱布尼茨公式”。

一、什么是微积分

圆的面积公式是什么？

其中S是圆的面积，π是圆周率，R是圆的半径。那么这个公式是怎么得到的？

首先，我们画一个圆，这个圆的半径为R，周长为C。我们知道，圆的周长与直径的比定义为圆周率，因此：

我们把圆分割成许多个小扇形，再然后，我们把这些扇形拼在一起，这样就形成了一个接近于长方形的图形。如下图：

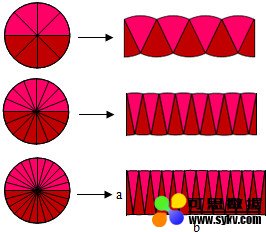
可以想象，如果圆分割的越细，拼好的图形就越接近长方形。如果圆分割成无限多份，那么拼起来就是一个严格的长方形了。

而且，这个长方形的面积与圆的面积是相等的。

我们要求圆的面积，只需要求出这个长方形的面积就可以了。这个长方形的宽就是圆的半径R，而长方形的长是圆周长的一半。

根据长方形的面积公式“长方形面积=长乘宽”，我们得到圆的面积公式：

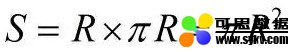
其实，这个推导过程很简单，那就是先无限分割，再把这无限多份求和。分割就是微分，求和就是积分，这就是微积分的基本思想。

1. 微分

由函数B=f（A），得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。

微分是函数改变量的线性主要部分，微积分的基本概念之一。

2. 积分

对于一个给定的正实值函数，在一个实数区间上的定积分可以理解为在坐标平面上，由曲线、直线以及轴围成的曲边梯形的面积值（一种确定的实数值）。

二、微积分的应用

1. 王元买瓜

不知道大家听没听说过王元买瓜的故事：

魏歪脖的西瓜卖得好，不称重，分大瓜小瓜卖，大瓜3块一个，小瓜1块一个。看到大瓜小瓜尺寸差别不是很大，所以很多人买小瓜。

王先生和王太太过来买瓜，王太太看了看打算挑一个小的，却听见王元先生说：“咱买那个大的。”

“大的贵3倍呢……”王太太犹豫。“大的比小的值。”王先生说。

王太太挑了两个大瓜，交了钱，看看别人都在抢小瓜，似乎又有些犹豫。王先生看出她犹豫，笑笑说：“你吃瓜吃的是什么？吃的是容积，不是面积。那小瓜的半径是大瓜的2／3稍弱，容积可是按立方算的。小的容积不到大的30％，当然买大的赚。”

王太太点点头，又摇摇头：“你算得不对，那大西瓜皮厚，小西瓜还皮薄呢，算容积，恐怕还是买大的吃亏。”

却见王先生胸有成竹，点点头道：“你别忘了那小西瓜的瓜皮却是3个瓜的，大西瓜只有1个，哪个皮多你再算算表面积看。”

王太太说：“头疼，我不算了。”两个人抱了西瓜回家，留下魏歪脖看得目瞪口呆。

这里稍微说一下，王元，著名数学家，院士，华罗庚数学奖得主，主要研究领域是解析数论。他曾任研究室主任、所长、所学术委员会主任、中国数学会理事长、《数学学报》主编，联邦德国《分析》杂志编辑。

这里西瓜皮的体积计算就要用到多重积分的知识，这个问题其实是计算大球和三个小球体积和的大小比较。我们知道球体检计算公式：